
Two identical magnetic dipoles of magnetic moment \[1.0A{m^2}\] each, placed at a separation of 2m with their axes perpendicular to each other. The resultant magnetic field at a point midway between the dipoles is
A. $\sqrt 5 \times {10^{ - 7}}T$
B. $5 \times {10^{ - 7}}T$
C. ${10^{ - 7}}T$
D. $2 \times {10^{ - 7}}T$
Answer
539.4k+ views
Hint: The axial and equatorial magnetic field would be perpendicular to each other. Since these are vector quantities, We have to take their vector sum. Use the equations ${\vec B_{ax}} = \dfrac{{{\mu _0}}}{{4\pi }}\dfrac{{2\vec m}}{{{r^3}}}$ and ${\vec B_{eq}} = \dfrac{{{\mu _0}}}{{4\pi }}\dfrac{{2\vec m}}{{{r^3}}}$
Complete step by step answer:
We know the magnetic field at an axial point on a dipole of magnetic moment $\vec m$ is given by :
$\overrightarrow {{B_1}} = \dfrac{{{\mu _0}}}{{4\pi }}\dfrac{{2\vec m}}{{{r^3}}}$ where r is the distance from centre of dipole to the axial point.
Similarly, the Magnetic field at an equatorial point, located along the perpendicular bisector of dipole is given as:
$\overrightarrow {{B_2}} = \dfrac{{{\mu _0}}}{{4\pi }}\dfrac{{\vec m}}{{{r^3}}}$
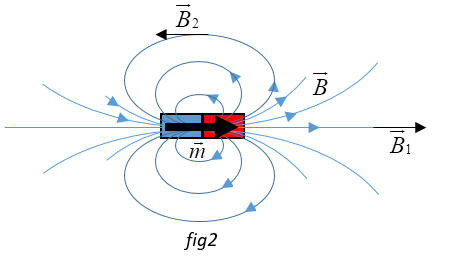
Also, the direction of $\vec B$ can easily be obtained by imagining field lines corresponding to the magnetic moment. (refer fig 2)
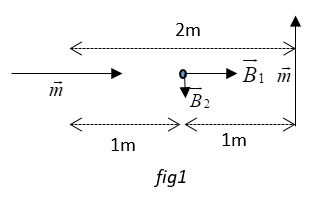
In this question, the magnetic field at point A due to the axial dipole would be a vector along the axis and that of the equatorial dipole would be perpendicular to the axis. (refer fig1)
The strength of axial field is:
$\left| {\overrightarrow {{B_1}} } \right|{\mkern 1mu} = \dfrac{{{\mu _0}}}{{4\pi }}\dfrac{{2 \times 1}}{{{1^3}}} = \dfrac{{2{\mu _0}}}{{4\pi }}$
The strength of equatorial field :
\[\left| {\overrightarrow {{B_2}} } \right|\, = \dfrac{{{\mu _0}}}{{4\pi }}\dfrac{1}{{{1^3}}} = \dfrac{{{\mu _0}}}{{4\pi }}\]
Now, the net magnetic field at A would be $\overrightarrow {{B_1}} + \overrightarrow {{B_2}} $
Since these vectors are perpendicular, the net magnetic field is given by :
${B_{net}} = \sqrt {{B_1}^2 + {B_2}^2} = \dfrac{{{\mu _0}}}{{4\pi }}\sqrt {{2^2} + {1^2}} = \dfrac{{\sqrt 5 {\mu _0}}}{{4\pi }}$
So the answer is $\sqrt 5 \times {10^{ - 7}}$
Additional Information:
The magnetic moment of a magnetic substance could be defined in two ways:
If the magnetic field is a result if a known current flowing through a loop of area A
then $\vec m = I \times \vec A$
If the field is que to a permanent magnet of length L, then
$\vec m = {q_m}2\vec l$
Here ${q_m}$ is the pole strength of a magnet and unlike electric charges, ${q_m}$ does not occur isolated. It always found in pairs as $ \pm {q_m}$
Note: Though the magnetic moment vector is drawn from the south to the north pole of a magnet, it shows the same direction as that of the magnetic field. This is because, inside a magnet, magnetic fields are from south to north.
Complete step by step answer:
We know the magnetic field at an axial point on a dipole of magnetic moment $\vec m$ is given by :
$\overrightarrow {{B_1}} = \dfrac{{{\mu _0}}}{{4\pi }}\dfrac{{2\vec m}}{{{r^3}}}$ where r is the distance from centre of dipole to the axial point.
Similarly, the Magnetic field at an equatorial point, located along the perpendicular bisector of dipole is given as:
$\overrightarrow {{B_2}} = \dfrac{{{\mu _0}}}{{4\pi }}\dfrac{{\vec m}}{{{r^3}}}$
Also, the direction of $\vec B$ can easily be obtained by imagining field lines corresponding to the magnetic moment. (refer fig 2)


In this question, the magnetic field at point A due to the axial dipole would be a vector along the axis and that of the equatorial dipole would be perpendicular to the axis. (refer fig1)
The strength of axial field is:
$\left| {\overrightarrow {{B_1}} } \right|{\mkern 1mu} = \dfrac{{{\mu _0}}}{{4\pi }}\dfrac{{2 \times 1}}{{{1^3}}} = \dfrac{{2{\mu _0}}}{{4\pi }}$
The strength of equatorial field :
\[\left| {\overrightarrow {{B_2}} } \right|\, = \dfrac{{{\mu _0}}}{{4\pi }}\dfrac{1}{{{1^3}}} = \dfrac{{{\mu _0}}}{{4\pi }}\]
Now, the net magnetic field at A would be $\overrightarrow {{B_1}} + \overrightarrow {{B_2}} $
Since these vectors are perpendicular, the net magnetic field is given by :
${B_{net}} = \sqrt {{B_1}^2 + {B_2}^2} = \dfrac{{{\mu _0}}}{{4\pi }}\sqrt {{2^2} + {1^2}} = \dfrac{{\sqrt 5 {\mu _0}}}{{4\pi }}$
So the answer is $\sqrt 5 \times {10^{ - 7}}$
Additional Information:
The magnetic moment of a magnetic substance could be defined in two ways:
If the magnetic field is a result if a known current flowing through a loop of area A
then $\vec m = I \times \vec A$
If the field is que to a permanent magnet of length L, then
$\vec m = {q_m}2\vec l$
Here ${q_m}$ is the pole strength of a magnet and unlike electric charges, ${q_m}$ does not occur isolated. It always found in pairs as $ \pm {q_m}$
Note: Though the magnetic moment vector is drawn from the south to the north pole of a magnet, it shows the same direction as that of the magnetic field. This is because, inside a magnet, magnetic fields are from south to north.
Recently Updated Pages
NCERT Solutions For Class 9 Hindi Sanchayan - Hammid Khan

NCERT Solutions For Class 6 Maths The Other Side Of Zero Exercise 10.2

Class 1 English Grammar Pronouns Worksheet PDF – Free Download

Class 1 Reading Comprehension Sentences Worksheet PDF

Area of Rectangle Worksheet for Class 3 Maths | Free PDF

Class 5 Long Division Worksheet: 2-Digit Divisors & Remainders

Trending doubts
Which are the Top 10 Largest Countries of the World?

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE

Why is the cell called the structural and functional class 12 biology CBSE

a Tabulate the differences in the characteristics of class 12 chemistry CBSE

Who discovered the cell and how class 12 biology CBSE

Draw a labelled sketch of the human eye class 12 physics CBSE




