
Triangle ABC is a right triangle with sides of length 4, 6 and x. If 4 < x < 6, what is the approximate value of x ?
A. 4
B. 4.47
C. 5.21
D. 5.63
E. 7.21
Answer
549k+ views
Hint: We have to only use the property of triangles that the length of the side opposite to the longest angle of the triangle is greatest. And had to use the Pythagorean theorem \[\left[ {{{\left( {{\text{Hypotenuse}}} \right)}^2} = {{\left( {{\text{Perpendicular}}} \right)}^2} + {{\left( {{\text{Base}}} \right)}^2}} \right]\] to find the value of x.
Complete step-by-step answer:
As we know that ABC is a right-angled triangle.
And the maximum angle of the right-angled triangle is 90 degrees. And the side which is opposite to the 90 degrees angle is the hypotenuse of that triangle.
So, from the property of the triangle which states that the side opposite to the greatest angle of the triangle Is greatest.
Greatest side of the right-angled triangle is the hypotenuse of the triangle.
As we know that sides of the triangle are 4, 5 and x. where 4 < x < 6.
So, the length of the hypotenuse of the triangle ABC will be equal to 6.
Now as we know that according to the Pythagorean theorem if XYZ is a Pythagoras triangle, right angled at Y. Then the square of its hypotenuse (XZ) is equal to the sum of squares of its other two sides (XY and YZ).
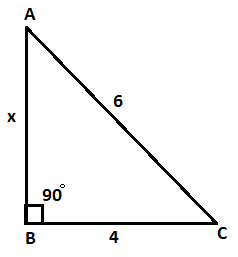
So, applying Pythagorean theorem in triangle ABC. We get,
\[
A{C^2} = A{B^2} + B{C^2} \\
{\left( 6 \right)^2} = {x^2} + {\left( 4 \right)^2} \\
36 = {x^2} + 16 \\
\]
Now subtracting 16 from both sides of the above equation. We get,
\[
{x^2} = 20 \\
x = \sqrt {20} \approx 4.47 \\
\]
x is positive length is always positive.
Hence, the correct option will be B.
Note: Whenever we come up with this type of problem then we use the property of right-angled triangle that the greatest side is the hypotenuse of the triangle to find the hypotenuse of the triangle. After that we will apply the Pythagorean theorem to find the third side of the triangle. At last we can approximate our answer up to two decimal places.
Complete step-by-step answer:
As we know that ABC is a right-angled triangle.
And the maximum angle of the right-angled triangle is 90 degrees. And the side which is opposite to the 90 degrees angle is the hypotenuse of that triangle.
So, from the property of the triangle which states that the side opposite to the greatest angle of the triangle Is greatest.
Greatest side of the right-angled triangle is the hypotenuse of the triangle.
As we know that sides of the triangle are 4, 5 and x. where 4 < x < 6.
So, the length of the hypotenuse of the triangle ABC will be equal to 6.
Now as we know that according to the Pythagorean theorem if XYZ is a Pythagoras triangle, right angled at Y. Then the square of its hypotenuse (XZ) is equal to the sum of squares of its other two sides (XY and YZ).

So, applying Pythagorean theorem in triangle ABC. We get,
\[
A{C^2} = A{B^2} + B{C^2} \\
{\left( 6 \right)^2} = {x^2} + {\left( 4 \right)^2} \\
36 = {x^2} + 16 \\
\]
Now subtracting 16 from both sides of the above equation. We get,
\[
{x^2} = 20 \\
x = \sqrt {20} \approx 4.47 \\
\]
x is positive length is always positive.
Hence, the correct option will be B.
Note: Whenever we come up with this type of problem then we use the property of right-angled triangle that the greatest side is the hypotenuse of the triangle to find the hypotenuse of the triangle. After that we will apply the Pythagorean theorem to find the third side of the triangle. At last we can approximate our answer up to two decimal places.
Recently Updated Pages
Master Class 10 English: Engaging Questions & Answers for Success

Master Class 10 Social Science: Engaging Questions & Answers for Success

Master Class 10 Maths: Engaging Questions & Answers for Success

Master Class 10 Science: Engaging Questions & Answers for Success

Class 10 Question and Answer - Your Ultimate Solutions Guide

Master Class 11 Economics: Engaging Questions & Answers for Success

Trending doubts
Why is there a time difference of about 5 hours between class 10 social science CBSE

What is the scientific name of apple class 10 biology CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

Fill the blanks with proper collective nouns 1 A of class 10 english CBSE

Write examples of herbivores carnivores and omnivo class 10 biology CBSE

Give 10 examples of Material nouns Abstract nouns Common class 10 english CBSE




