
The surface charge density of a thin charged disc of radius R is σ. The value of the electric field at the center of the disc is $\dfrac{\sigma }{2{{\in }_{0}}}$. With respect to the field at the center of the electric field along the axis at a distance R from the center of the disc
A. Reduces by 70.7%
B. Reduces by 29.3%
C. Reduces by 9.7%
D. Reduces by 14.6%
Answer
535.5k+ views
Hint: This can be solved by using the electric field due to a uniformly charged disc formula. We shall substitute the given values of radius and electric field at the center of the disc to find the electric field along the axis.
Complete step-by-step answer:
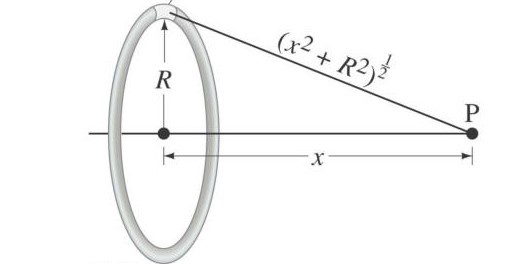
The general expression for an electric field due to a uniformly charged disc of radius R and charge density σ can be written as
${{E}_{x}}=k\sigma 2\pi \left( 1-\dfrac{x}{\sqrt{{{x}^{2}}+{{R}^{2}}}} \right)$
Where, $k=\dfrac{1}{4\pi {{\in }_{0}}}$
On substituting ‘k’ in the formula, we get
${{E}_{x}}=\dfrac{\sigma }{2{{\in }_{0}}}\left( 1-\dfrac{x}{\sqrt{{{x}^{2}}+{{R}^{2}}}} \right)$
Here, the given electric field intensity at the center of the disc shall be ‘E’ i.e., $x=0$,
$E=\dfrac{\sigma }{2{{\in }_{0}}}$
Let electric field along the axis at a distance ‘x’ from the center of the disc be ‘E1’ and written as
${{E}_{1}}=\dfrac{\sigma }{2{{\in }_{0}}}\left( 1-\dfrac{x}{\sqrt{{{x}^{2}}+{{R}^{2}}}} \right)$
As $x=R$, the equation becomes
${{E}_{1}}=\dfrac{\sigma }{2{{\in }_{0}}}\left( 1-\dfrac{R}{\sqrt{{{R}^{2}}+{{R}^{2}}}} \right)$
${{E}_{1}}=\dfrac{\sigma }{2{{\in }_{0}}}\left( 1-\dfrac{R}{\sqrt{2}R} \right)$
On taking ‘R’ common, it gets cancelled
${{E}_{1}}=\dfrac{\sigma }{2{{\in }_{0}}}\left( 1-\dfrac{1}{\sqrt{2}} \right)$
We also know, $E=\dfrac{\sigma }{2{{\in }_{0}}}$
On substituting ‘E’ in the equation, we get
${{E}_{1}}=E\left( 1-\dfrac{1}{\sqrt{2}} \right)$
The percentage of reduction in the value of electric field can be calculated as
$=\dfrac{{{E}_{1}}-E}{E}\times 100$
$=\dfrac{\left( E\left( 1-\dfrac{1}{\sqrt{2}} \right)-E \right)}{E}\times 100$
$=\left( 1-\dfrac{1}{\sqrt{2}}-1 \right)\times 100$
$=-\dfrac{100}{\sqrt{2}}=70.7%$
The negative sign indicates the reduction.
Therefore, the correct answer for the given question is option (A).
Note: The electric field due to a uniformly charged disc is based on the applications of gauss’s law. The law states that the total flux of electric field over a closed surface is equal to $\dfrac{1}{{{\in }_{0}}}$ times the total charge enclosed by the surface.
Complete step-by-step answer:

The general expression for an electric field due to a uniformly charged disc of radius R and charge density σ can be written as
${{E}_{x}}=k\sigma 2\pi \left( 1-\dfrac{x}{\sqrt{{{x}^{2}}+{{R}^{2}}}} \right)$
Where, $k=\dfrac{1}{4\pi {{\in }_{0}}}$
On substituting ‘k’ in the formula, we get
${{E}_{x}}=\dfrac{\sigma }{2{{\in }_{0}}}\left( 1-\dfrac{x}{\sqrt{{{x}^{2}}+{{R}^{2}}}} \right)$
Here, the given electric field intensity at the center of the disc shall be ‘E’ i.e., $x=0$,
$E=\dfrac{\sigma }{2{{\in }_{0}}}$
Let electric field along the axis at a distance ‘x’ from the center of the disc be ‘E1’ and written as
${{E}_{1}}=\dfrac{\sigma }{2{{\in }_{0}}}\left( 1-\dfrac{x}{\sqrt{{{x}^{2}}+{{R}^{2}}}} \right)$
As $x=R$, the equation becomes
${{E}_{1}}=\dfrac{\sigma }{2{{\in }_{0}}}\left( 1-\dfrac{R}{\sqrt{{{R}^{2}}+{{R}^{2}}}} \right)$
${{E}_{1}}=\dfrac{\sigma }{2{{\in }_{0}}}\left( 1-\dfrac{R}{\sqrt{2}R} \right)$
On taking ‘R’ common, it gets cancelled
${{E}_{1}}=\dfrac{\sigma }{2{{\in }_{0}}}\left( 1-\dfrac{1}{\sqrt{2}} \right)$
We also know, $E=\dfrac{\sigma }{2{{\in }_{0}}}$
On substituting ‘E’ in the equation, we get
${{E}_{1}}=E\left( 1-\dfrac{1}{\sqrt{2}} \right)$
The percentage of reduction in the value of electric field can be calculated as
$=\dfrac{{{E}_{1}}-E}{E}\times 100$
$=\dfrac{\left( E\left( 1-\dfrac{1}{\sqrt{2}} \right)-E \right)}{E}\times 100$
$=\left( 1-\dfrac{1}{\sqrt{2}}-1 \right)\times 100$
$=-\dfrac{100}{\sqrt{2}}=70.7%$
The negative sign indicates the reduction.
Therefore, the correct answer for the given question is option (A).
Note: The electric field due to a uniformly charged disc is based on the applications of gauss’s law. The law states that the total flux of electric field over a closed surface is equal to $\dfrac{1}{{{\in }_{0}}}$ times the total charge enclosed by the surface.
Recently Updated Pages
Master Class 12 Biology: Engaging Questions & Answers for Success

Master Class 12 Physics: Engaging Questions & Answers for Success

Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Trending doubts
Which are the Top 10 Largest Countries of the World?

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE

Why is the cell called the structural and functional class 12 biology CBSE

a Tabulate the differences in the characteristics of class 12 chemistry CBSE

Who discovered the cell and how class 12 biology CBSE

Draw a labelled sketch of the human eye class 12 physics CBSE




