
The stress versus strain graphs for wires of two materials A and B are as shown in the figure.
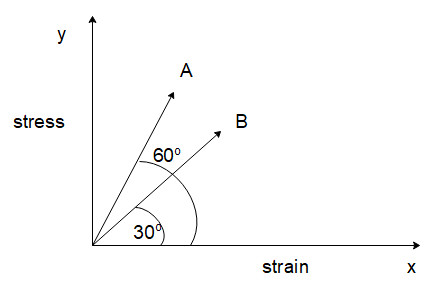
If $ {Y_A} $ and $ {Y_B} $ are the Young’s moduli of the materials, then
A) $ {Y_B} = 2{Y_A} $
B) $ {Y_A} = {Y_B} $
C) $ {Y_B} = 3{Y_A} $
D) $ {Y_A} = 3{Y_B} $

Answer
546.3k+ views
Hint : The young’s modulus of wire is the slope of the line of the wire in the graph of stress versus strain. The slope of a line can be determined using the angle the line makes with the $ x $ -axis.
Complete step by step answer
We know that the slope of the line in a stress-strain curve represents the young’s modulus for a wire. We also know that the slope of a line can be calculated as the tangent of the angle the line makes with the positive x-axis of the graph.
So, for wire A, the stress-strain line of the material is at an angle of $ 60^\circ $ from the positive $ x $ -axis. So the slope of the line $ ({m_A}) $ will be
$ {m_A} = \tan 60^\circ $
$ \Rightarrow {m_A} = \sqrt 3 $
Hence the young’s modulus of wire A will also be $ \sqrt 3 $ .
Similarly, for wire B, the stress-strain line of the material is at an angle of $ 30^\circ $ from the positive $ x $ -axis. So, the slope of the line $ ({m_B}) $ will be
$ {m_B} = \tan 30^\circ $
$ \Rightarrow {m_B} = \dfrac{1}{{\sqrt 3 }} $
Hence the young’s modulus of wire B will also be $ 1/\sqrt 3 $ .
Then taking the ratio of the young’s modulus for wire A and B, we get
$ \dfrac{{{Y_A}}}{{{Y_B}}} = \dfrac{{\sqrt 3 }}{{1/\sqrt 3 }} $
$ \therefore \dfrac{{{Y_A}}}{{{Y_B}}} = 3 $
Hence, we can write
$ {Y_A} = 3{Y_B} $ which corresponds to option (D) which is the correct choice.
Note
We can only calculate the slope of the line in such a way if the stress-strain curve for a wire is a straight line. For practical wires, the stress-strain curve is linear only for a range of values of stress applied on the wire. While calculating the slope of the wire, we must calculate the tangent of the line made with the $ x $ -axis and not the $ y $ -axis if the strain is represented on the $ x $ -axis of the graph.
Complete step by step answer
We know that the slope of the line in a stress-strain curve represents the young’s modulus for a wire. We also know that the slope of a line can be calculated as the tangent of the angle the line makes with the positive x-axis of the graph.
So, for wire A, the stress-strain line of the material is at an angle of $ 60^\circ $ from the positive $ x $ -axis. So the slope of the line $ ({m_A}) $ will be
$ {m_A} = \tan 60^\circ $
$ \Rightarrow {m_A} = \sqrt 3 $
Hence the young’s modulus of wire A will also be $ \sqrt 3 $ .
Similarly, for wire B, the stress-strain line of the material is at an angle of $ 30^\circ $ from the positive $ x $ -axis. So, the slope of the line $ ({m_B}) $ will be
$ {m_B} = \tan 30^\circ $
$ \Rightarrow {m_B} = \dfrac{1}{{\sqrt 3 }} $
Hence the young’s modulus of wire B will also be $ 1/\sqrt 3 $ .
Then taking the ratio of the young’s modulus for wire A and B, we get
$ \dfrac{{{Y_A}}}{{{Y_B}}} = \dfrac{{\sqrt 3 }}{{1/\sqrt 3 }} $
$ \therefore \dfrac{{{Y_A}}}{{{Y_B}}} = 3 $
Hence, we can write
$ {Y_A} = 3{Y_B} $ which corresponds to option (D) which is the correct choice.
Note
We can only calculate the slope of the line in such a way if the stress-strain curve for a wire is a straight line. For practical wires, the stress-strain curve is linear only for a range of values of stress applied on the wire. While calculating the slope of the wire, we must calculate the tangent of the line made with the $ x $ -axis and not the $ y $ -axis if the strain is represented on the $ x $ -axis of the graph.
Recently Updated Pages
Why is there a time difference of about 5 hours between class 10 social science CBSE

In cricket, what is a "pink ball" primarily used for?

In cricket, what is the "new ball" phase?

In cricket, what is a "death over"?

What is the "Powerplay" in T20 cricket?

In cricket, what is a "super over"?

Trending doubts
What is meant by exothermic and endothermic reactions class 11 chemistry CBSE

Which animal has three hearts class 11 biology CBSE

10 examples of friction in our daily life

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells




