
The image distance of an object placed \[10cm\] in front of a thin lens of focal length \[+5cm\]
Answer
514.2k+ views
Hint: The relation between object distance, image distance and focal length is given by the lens formula. Substituting corresponding values in the lens formula and putting the correct sign for each by following the sign convention will give us the required value of image distance.
Formulas Used:
\[\dfrac{1}{v}-\dfrac{1}{u}=\dfrac{1}{f}\]
Complete answer:
Refraction is the bending of rays of light when it passes from one medium to the other. When light passes through a lens, it undergoes refraction.
Given- focal length is \[+5cm\]. This means that it is a convex lens as convex lenses have positive focal lengths.
By convention all distances in front of the lens are taken as positive and distances behind the lens are taken as negative. Therefore, image distance in a convex lens is positive but object distance is negative.
The Lens formula is given by-
\[\dfrac{1}{v}-\dfrac{1}{u}=\dfrac{1}{f}\] - (1)
Here, \[v\] is the image distance from the centre of lens
\[u\] is the object distance from center of lens
\[f\] is focal length of the lens
Substituting the given values in eq (1), we have,
\[\begin{align}
& \dfrac{1}{v}-\dfrac{1}{-10}=\dfrac{1}{5} \\
& \dfrac{1}{v}=\dfrac{1}{5}-\dfrac{1}{10} \\
& \Rightarrow \dfrac{1}{v}=\dfrac{1}{10} \\
\end{align}\]
\[\therefore v=10cm\] - (2)
The image distance is \[10cm\] in front of the lens, this is equal to object distance behind the lens. The image is formed at \[2f\], it is real, inverted and the same size as the object
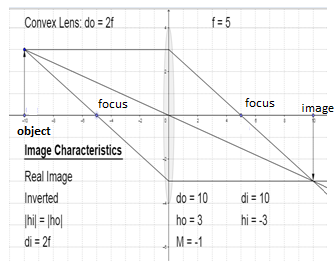
Here,
\[{{d}_{o}}\] is the object distance
\[{{d}_{i}}\] is the image distance
\[{{h}_{o}}\] is the object height
\[{{h}_{i}}\] is the image height
\[M\] is the magnification, that is, ratio of image height to object height
Note:
There are different image formations in a convex lens. It forms a virtual image if the object distance is \[u2f\] the image formed is diminished, real and inverted and formed beyond \[2f\].
Formulas Used:
\[\dfrac{1}{v}-\dfrac{1}{u}=\dfrac{1}{f}\]
Complete answer:
Refraction is the bending of rays of light when it passes from one medium to the other. When light passes through a lens, it undergoes refraction.

Given- focal length is \[+5cm\]. This means that it is a convex lens as convex lenses have positive focal lengths.
By convention all distances in front of the lens are taken as positive and distances behind the lens are taken as negative. Therefore, image distance in a convex lens is positive but object distance is negative.
The Lens formula is given by-
\[\dfrac{1}{v}-\dfrac{1}{u}=\dfrac{1}{f}\] - (1)
Here, \[v\] is the image distance from the centre of lens
\[u\] is the object distance from center of lens
\[f\] is focal length of the lens
Substituting the given values in eq (1), we have,
\[\begin{align}
& \dfrac{1}{v}-\dfrac{1}{-10}=\dfrac{1}{5} \\
& \dfrac{1}{v}=\dfrac{1}{5}-\dfrac{1}{10} \\
& \Rightarrow \dfrac{1}{v}=\dfrac{1}{10} \\
\end{align}\]
\[\therefore v=10cm\] - (2)
The image distance is \[10cm\] in front of the lens, this is equal to object distance behind the lens. The image is formed at \[2f\], it is real, inverted and the same size as the object

Here,
\[{{d}_{o}}\] is the object distance
\[{{d}_{i}}\] is the image distance
\[{{h}_{o}}\] is the object height
\[{{h}_{i}}\] is the image height
\[M\] is the magnification, that is, ratio of image height to object height
Note:
There are different image formations in a convex lens. It forms a virtual image if the object distance is \[u
Recently Updated Pages
Ncert Books Class 10 Science Chapter 2 Free Download

Ncert Books Class 11 Biology Chapter 16 Free Download

Ncert Books Class 11 Biology Chapter 12 Free Download

Ncert Books Class 11 Biology Chapter 10 Free Download

Ncert Books Class 11 Chemistry Chapter 7 Free Download

Ncert Books Class 11 Physics Chapter 8 Free Download

Trending doubts
Which are the Top 10 Largest Countries of the World?

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE

Why is the cell called the structural and functional class 12 biology CBSE

a Tabulate the differences in the characteristics of class 12 chemistry CBSE

Who discovered the cell and how class 12 biology CBSE

Draw a labelled sketch of the human eye class 12 physics CBSE




