
Answer
463.5k+ views
Hint:To solve this particular problem we have to first visualize the situation. There are different forces in action over the balloon. It is advised to draw each case which will give us a better perception of the solution to this problem.
Complete step by step answer:
Let M be the mass of the balloon.
Let the air resistance force on the balloon be F.
Given that the force of air resistance is proportional to the velocity, so we can write,
$F \propto v$ .
This can be rewritten as,
$F = kv$,
where k = proportionality constant.
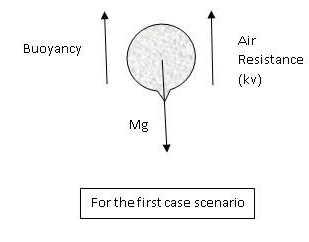
Now, considering the first scenario where the balloon is moving towards the ground at a constant velocity v, we can see from the figure that three forces are working on the balloon. Force of gravity (Mg), Buoyancy(B), and Air resistance (kv). As the balloon is falling at a constant velocity, all these three velocities must cancel each other thus considering the direction of the force we can write,
$B + kv = Mg$ .
This can be rewritten as,
$M = \dfrac{{B + kv}}{g}$.
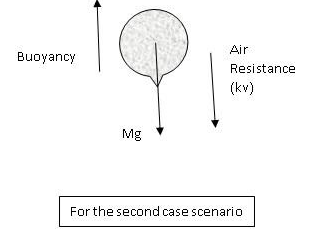
Now, in the second scenario where due to the reduction in mass the balloon starts rising at a constant velocity v. In this case let the Mass be $M'$.
In this case also as the balloon is rising at a constant velocity, all these three velocities must cancel each other thus considering the direction of the force we can write,
$B = M'g + kv$ .
This equation can be rewritten as,
$M' = \dfrac{{B - kv}}{g}$
Thus, the amount of mass to be removed for the balloon to rise can be given as,
$\Delta M = M - M'$
Putting the values of M and $M'$from the above equations we get,
$\Delta M = \dfrac{{B + kv}}{g} - \dfrac{{B - kv}}{g}$
Solving this equation, we get,
$\Delta M = \dfrac{{B + kv - B + kv}}{g} = \dfrac{{2kv}}{g}$. ----(1)
Again, from the first scenario we get,
$B + kv = Mg$,
This can be also written as $kv = Mg - B$ .
Putting this value in (1) we get,
$\Delta M = \dfrac{{2(Mg - B)}}{g} = 2(M - \dfrac{B}{g})$ .
Thus, to make the balloon move in an upward direction with a constant velocity v, we have to reduce a mass of $\dfrac{B}{g}$.
Note:This is a very conceptual question so it has to be solved very nicely using all the necessary diagrams/ figures. It is suggested for all students to draw figures to calculate for this kind of problem as it is very easy to make an error in this kind of question.
Complete step by step answer:
Let M be the mass of the balloon.
Let the air resistance force on the balloon be F.
Given that the force of air resistance is proportional to the velocity, so we can write,
$F \propto v$ .
This can be rewritten as,
$F = kv$,
where k = proportionality constant.

Now, considering the first scenario where the balloon is moving towards the ground at a constant velocity v, we can see from the figure that three forces are working on the balloon. Force of gravity (Mg), Buoyancy(B), and Air resistance (kv). As the balloon is falling at a constant velocity, all these three velocities must cancel each other thus considering the direction of the force we can write,
$B + kv = Mg$ .
This can be rewritten as,
$M = \dfrac{{B + kv}}{g}$.

Now, in the second scenario where due to the reduction in mass the balloon starts rising at a constant velocity v. In this case let the Mass be $M'$.
In this case also as the balloon is rising at a constant velocity, all these three velocities must cancel each other thus considering the direction of the force we can write,
$B = M'g + kv$ .
This equation can be rewritten as,
$M' = \dfrac{{B - kv}}{g}$
Thus, the amount of mass to be removed for the balloon to rise can be given as,
$\Delta M = M - M'$
Putting the values of M and $M'$from the above equations we get,
$\Delta M = \dfrac{{B + kv}}{g} - \dfrac{{B - kv}}{g}$
Solving this equation, we get,
$\Delta M = \dfrac{{B + kv - B + kv}}{g} = \dfrac{{2kv}}{g}$. ----(1)
Again, from the first scenario we get,
$B + kv = Mg$,
This can be also written as $kv = Mg - B$ .
Putting this value in (1) we get,
$\Delta M = \dfrac{{2(Mg - B)}}{g} = 2(M - \dfrac{B}{g})$ .
Thus, to make the balloon move in an upward direction with a constant velocity v, we have to reduce a mass of $\dfrac{B}{g}$.
Note:This is a very conceptual question so it has to be solved very nicely using all the necessary diagrams/ figures. It is suggested for all students to draw figures to calculate for this kind of problem as it is very easy to make an error in this kind of question.
Recently Updated Pages
How is abiogenesis theory disproved experimentally class 12 biology CBSE

What is Biological Magnification

Explain the Basics of Computer and Number System?

Class 11 Question and Answer - Your Ultimate Solutions Guide

Write the IUPAC name of the given compound class 11 chemistry CBSE

Write the IUPAC name of the given compound class 11 chemistry CBSE

Trending doubts
Proton was discovered by A Thomson B Rutherford C Chadwick class 11 chemistry CBSE

What organs are located on the left side of your body class 11 biology CBSE

How many squares are there in a chess board A 1296 class 11 maths CBSE

State the laws of reflection of light

What are ekaboron ekaaluminium and ekasilicon class 11 chemistry CBSE

Three moles of B2H6 are completely reacted with methanol class 11 chemistry CBSE




