
The dimension of coefficient of viscosity $\eta $ is:
Answer
575.4k+ views
HintIt is based on the concept of dimensional analysis which is used to represent the physical quantities in the form of dimensional expression. The fundamental physical quantities represented by the suitable symbols as following Table shows:
Complete step-by-step solution:
To find the dimension, it is necessary that we have knowledge of relation of given physical quantities with the other fundamental quantities.
1) For dimension first we describe what is viscosity and on which physical quantities it depends. It is the property of fluids (liquids and gases) that opposes the flow of fluids. Suppose liquid is in streamline flow and divides into different layer of molecules, with velocities
${v_1} < {v_2} < {v_3} < ...........$
Here we observe that, there is relative motion between any two layers, which are in contact. Hence the opposing (contact or friction) force acting between the layers, this opposing force (F) is directly proportional to the area (A) of layers, i.e.
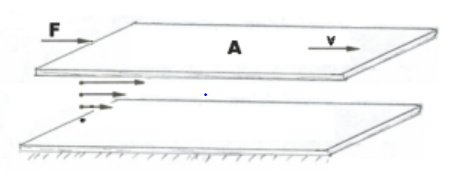
${\text{F}}\alpha {\text{A}}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \to {\text{(1)}}$
(As the area increases the opposing force is also increased)
Further we also observe that the layers of liquid which are in contact with solid surface has the relative velocity zero, as we go up the relative velocity of layers increases , thus between two successive layers at distance $(dx)$having relative velocity $(dv)$
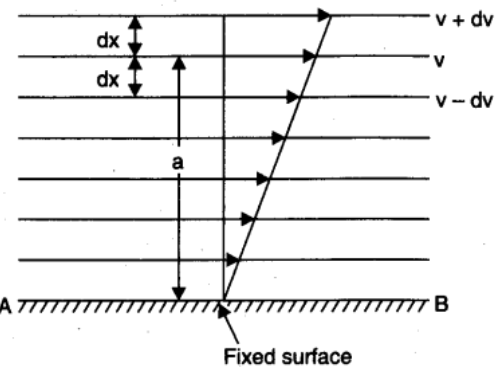
Hence the relative velocity per unit distance i.e. velocity gradient\[ = \dfrac{{dv}}{{dx}}\]
The opposing force between the layers is directly proportional to the velocity gradient i.e.
${\text{F}}\alpha - \dfrac{{dv}}{{dx}}\,\,\,\,\,\,\,\,\,\,\,\,\,\, \to {\text{(2)}}$
(Negative sign indicates the force is opposite direction to velocity of layers)
From equation (1) and (2)
${\text{F}}\alpha - A\dfrac{{dv}}{{dx}}$
${\text{F = }} - \eta A\dfrac{{dv}}{{dx}}$
Hence $\eta $ is the coefficient of viscosity.
2) Using equation (3)
$\eta = \dfrac{{ - F}}{{A\dfrac{{dv}}{{dx}}}}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(4)$
First we write dimensions of each physical quantities:
Remember that each derived physical quantity breaks into its related physical quantity.
(i) Force: $F = ma = m\dfrac{v}{t} = m\dfrac{x}{{t.t}}$
Write corresponding symbol from table
$
F = \dfrac{{\left[ M \right]\left[ L \right]}}{{{{\left[ T \right]}^2}}} \\
F = \left[ M \right]\left[ L \right]{\left[ T \right]^{ - 2}} \\
$
(ii) Area: $A = l \times b$
Write corresponding symbol from table
$A = \left[ L \right]\left[ L \right] = {\left[ L \right]^2}$
(iii) Velocity gradient: $\dfrac{{dv}}{{dx}} = \dfrac{{\dfrac{{dx}}{{dt}}}}{{dx}} = \dfrac{1}{{dt}}$
Write corresponding symbol from table
$\dfrac{{dv}}{{dx}} = \dfrac{1}{{\left[ T \right]}} = {\left[ T \right]^{ - 1}}$
Put the dimensions of F, T and $\dfrac{{dv}}{{dx}}$in equation (4)(ignore the negative sign)
$
\eta = \dfrac{{ - \left[ {ML{T^{ - 2}}} \right]}}{{\left[ {{M^2}} \right]\left[ {{T^{ - 1}}} \right]}} \\
\,\eta = \left[ {M{L^{ - 1}}{T^{ - 1}}} \right] \\
$
Note:- It is necessary to have the knowledge of dimensions with its limitations. Application of dimension is also useful for explanation of relation between physical quantities.
| Physical Quantities | Symbol |
| Mass | M |
| Time | T |
| Length | L |
| Electric Current | A |
| Temperature | $\Theta$ |
Complete step-by-step solution:
To find the dimension, it is necessary that we have knowledge of relation of given physical quantities with the other fundamental quantities.
1) For dimension first we describe what is viscosity and on which physical quantities it depends. It is the property of fluids (liquids and gases) that opposes the flow of fluids. Suppose liquid is in streamline flow and divides into different layer of molecules, with velocities
${v_1} < {v_2} < {v_3} < ...........$
Here we observe that, there is relative motion between any two layers, which are in contact. Hence the opposing (contact or friction) force acting between the layers, this opposing force (F) is directly proportional to the area (A) of layers, i.e.

${\text{F}}\alpha {\text{A}}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \to {\text{(1)}}$
(As the area increases the opposing force is also increased)
Further we also observe that the layers of liquid which are in contact with solid surface has the relative velocity zero, as we go up the relative velocity of layers increases , thus between two successive layers at distance $(dx)$having relative velocity $(dv)$

Hence the relative velocity per unit distance i.e. velocity gradient\[ = \dfrac{{dv}}{{dx}}\]
The opposing force between the layers is directly proportional to the velocity gradient i.e.
${\text{F}}\alpha - \dfrac{{dv}}{{dx}}\,\,\,\,\,\,\,\,\,\,\,\,\,\, \to {\text{(2)}}$
(Negative sign indicates the force is opposite direction to velocity of layers)
From equation (1) and (2)
${\text{F}}\alpha - A\dfrac{{dv}}{{dx}}$
${\text{F = }} - \eta A\dfrac{{dv}}{{dx}}$
Hence $\eta $ is the coefficient of viscosity.
2) Using equation (3)
$\eta = \dfrac{{ - F}}{{A\dfrac{{dv}}{{dx}}}}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(4)$
First we write dimensions of each physical quantities:
Remember that each derived physical quantity breaks into its related physical quantity.
(i) Force: $F = ma = m\dfrac{v}{t} = m\dfrac{x}{{t.t}}$
Write corresponding symbol from table
$
F = \dfrac{{\left[ M \right]\left[ L \right]}}{{{{\left[ T \right]}^2}}} \\
F = \left[ M \right]\left[ L \right]{\left[ T \right]^{ - 2}} \\
$
(ii) Area: $A = l \times b$
Write corresponding symbol from table
$A = \left[ L \right]\left[ L \right] = {\left[ L \right]^2}$
(iii) Velocity gradient: $\dfrac{{dv}}{{dx}} = \dfrac{{\dfrac{{dx}}{{dt}}}}{{dx}} = \dfrac{1}{{dt}}$
Write corresponding symbol from table
$\dfrac{{dv}}{{dx}} = \dfrac{1}{{\left[ T \right]}} = {\left[ T \right]^{ - 1}}$
Put the dimensions of F, T and $\dfrac{{dv}}{{dx}}$in equation (4)(ignore the negative sign)
$
\eta = \dfrac{{ - \left[ {ML{T^{ - 2}}} \right]}}{{\left[ {{M^2}} \right]\left[ {{T^{ - 1}}} \right]}} \\
\,\eta = \left[ {M{L^{ - 1}}{T^{ - 1}}} \right] \\
$
Note:- It is necessary to have the knowledge of dimensions with its limitations. Application of dimension is also useful for explanation of relation between physical quantities.
Recently Updated Pages
Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 Science: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Trending doubts
Which are the Top 10 Largest Countries of the World?

Draw a labelled sketch of the human eye class 12 physics CBSE

State the principle of an ac generator and explain class 12 physics CBSE

Differentiate between insitu conservation and exsitu class 12 biology CBSE

Sketch the electric field lines in case of an electric class 12 physics CBSE

Give 10 examples of unisexual and bisexual flowers




