
The curved surface area of the cylindrical pillar is $264\,{{\text{m}}^{2}}$ and its volume is $924\text{ }{{\text{m}}^{3}}$. Find the diameter and the height of the pillar.
Answer
548.4k+ views
Hint: First, let us draw the diagram of a cylindrical wall as per the given conditions. Now, we will use the curved surface area $=2\pi \text{rh}$ and the volume of cylinder $=\pi {{\text{r}}^{2}}\text{h}$ and equate the radius and find the value of radius in terms of ‘h’. Find the value of ‘h’ by using basic mathematical operations, then, substitute the value of ‘h’ in the radius equation and find the value of radius which will give you the value of diameter (d = 2r).
Complete step-by-step solution
Let us first draw the figure of the cylindrical pillar mentioning the required variables and the given values.
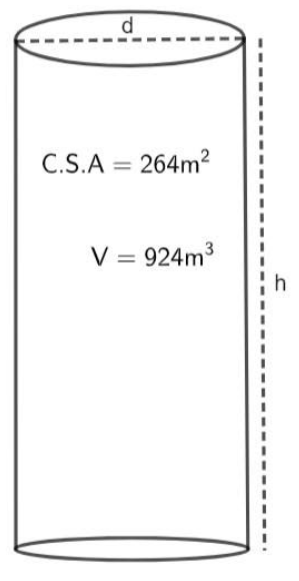
From the figure, we can see that the curved surface area is $264\ {{\text{m}}^{2}}$ and the volume of the cylindrical pillar is $924\,{{\text{m}}^{3}}$.
We know,
Curved surface area of the cylinder $=2\pi \text{rh}$
\[264=2\pi \text{rh}\]
Now, let us divide by $2\pi $ on both the sides of the equation, we get
$\begin{align}
& \dfrac{264}{2\pi }=\dfrac{2\pi \text{rh}}{2\pi } \\
&\Rightarrow 42.01=\text{rh}
\end{align}$
$\Rightarrow \text{r =}\dfrac{42.01}{\text{h}}$……… (1)
We know,
Volume of the cylinder $=\pi {{\text{r}}^{2}}\text{h}$
$924=\pi {{\text{r}}^{2}}\text{h}$
Divide by $\pi $ on both the sides of the equation, we get
$\begin{align}
&\Rightarrow \dfrac{924}{\pi }=\dfrac{\pi {{\text{r}}^{2}}\text{h}}{\pi } \\
&\Rightarrow 294.11={{\text{r}}^{2}}\text{h} \\
\end{align}$
$\Rightarrow {{\text{r}}^{2}}=\dfrac{294.11}{\text{h}}$
Taking the square root on both the sides, we get
$\text{r}\,\text{= }\sqrt{\dfrac{294.11}{\text{h}}}$………. (2)
From the equations (1) and (2), we get
$\dfrac{42.01}{\text{h}}$$\text{= }\sqrt{\dfrac{294.11}{\text{h}}}$
Now, after squaring on both the sides, we get
$\begin{align}
&\Rightarrow {{\left( \dfrac{42.01}{\text{h}} \right)}^{2}}={{\left( \sqrt{\dfrac{294.11}{\text{h}}} \right)}^{2}} \\
&\Rightarrow \dfrac{1764.84}{{{\text{h}}^{2}}}=\dfrac{294.11}{\text{h}} \\
&\Rightarrow \dfrac{1764.84}{\text{h}}=294.11 \\
&\Rightarrow \dfrac{1764.84}{294.11}=\text{h}
\end{align}$
$\Rightarrow \text{h = 6}\text{.0006}$
Therefore, the height of the cylindrical wall is approximately 6 m.
Now, let us substitute the value of height in equation (1), we get
$\begin{align}
& \text{r =}\dfrac{42.01}{\text{h}} \\
& =\dfrac{42.01}{6} \\
& =7.001
\end{align}$
Therefore, we got the value of radius, approximately 7 m.
We know,
Diameter = 2 (Radius)
= 2 (7)
= 14 m
Hence, the diameter of the cylindrical wall is 14 m and the height is 6 m.
Note: The bases of a cylinder are always congruent and parallel to each other. A cylinder is a three dimensional solid which is similar to the prism since it has a similar cross-section everywhere. To find the total surface area of the cylinder, you need to find the sum of the curved surface area of the cylinder and the area of two bases of the cylinder.
Complete step-by-step solution
Let us first draw the figure of the cylindrical pillar mentioning the required variables and the given values.

From the figure, we can see that the curved surface area is $264\ {{\text{m}}^{2}}$ and the volume of the cylindrical pillar is $924\,{{\text{m}}^{3}}$.
We know,
Curved surface area of the cylinder $=2\pi \text{rh}$
\[264=2\pi \text{rh}\]
Now, let us divide by $2\pi $ on both the sides of the equation, we get
$\begin{align}
& \dfrac{264}{2\pi }=\dfrac{2\pi \text{rh}}{2\pi } \\
&\Rightarrow 42.01=\text{rh}
\end{align}$
$\Rightarrow \text{r =}\dfrac{42.01}{\text{h}}$……… (1)
We know,
Volume of the cylinder $=\pi {{\text{r}}^{2}}\text{h}$
$924=\pi {{\text{r}}^{2}}\text{h}$
Divide by $\pi $ on both the sides of the equation, we get
$\begin{align}
&\Rightarrow \dfrac{924}{\pi }=\dfrac{\pi {{\text{r}}^{2}}\text{h}}{\pi } \\
&\Rightarrow 294.11={{\text{r}}^{2}}\text{h} \\
\end{align}$
$\Rightarrow {{\text{r}}^{2}}=\dfrac{294.11}{\text{h}}$
Taking the square root on both the sides, we get
$\text{r}\,\text{= }\sqrt{\dfrac{294.11}{\text{h}}}$………. (2)
From the equations (1) and (2), we get
$\dfrac{42.01}{\text{h}}$$\text{= }\sqrt{\dfrac{294.11}{\text{h}}}$
Now, after squaring on both the sides, we get
$\begin{align}
&\Rightarrow {{\left( \dfrac{42.01}{\text{h}} \right)}^{2}}={{\left( \sqrt{\dfrac{294.11}{\text{h}}} \right)}^{2}} \\
&\Rightarrow \dfrac{1764.84}{{{\text{h}}^{2}}}=\dfrac{294.11}{\text{h}} \\
&\Rightarrow \dfrac{1764.84}{\text{h}}=294.11 \\
&\Rightarrow \dfrac{1764.84}{294.11}=\text{h}
\end{align}$
$\Rightarrow \text{h = 6}\text{.0006}$
Therefore, the height of the cylindrical wall is approximately 6 m.
Now, let us substitute the value of height in equation (1), we get
$\begin{align}
& \text{r =}\dfrac{42.01}{\text{h}} \\
& =\dfrac{42.01}{6} \\
& =7.001
\end{align}$
Therefore, we got the value of radius, approximately 7 m.
We know,
Diameter = 2 (Radius)
= 2 (7)
= 14 m
Hence, the diameter of the cylindrical wall is 14 m and the height is 6 m.
Note: The bases of a cylinder are always congruent and parallel to each other. A cylinder is a three dimensional solid which is similar to the prism since it has a similar cross-section everywhere. To find the total surface area of the cylinder, you need to find the sum of the curved surface area of the cylinder and the area of two bases of the cylinder.
Recently Updated Pages
How do you convert r6sec theta into Cartesian form class 10 maths CBSE

How do you solve dfrac5y3dfracy+72y6+1 and find any class 10 maths CBSE

If sin A+B1 and cos AB1 0circ le left A+B rightle 90circ class 10 maths CBSE

On the number line 10 is to the of zero class 10 maths CBSE

How do you solve 5xge 30 class 10 maths CBSE

In the following sentence supply a verb in agreement class 10 english CBSE

Trending doubts
Write an application to the principal requesting five class 10 english CBSE

Why is there a time difference of about 5 hours between class 10 social science CBSE

Write a letter to the principal requesting him to grant class 10 english CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

What is the median of the first 10 natural numbers class 10 maths CBSE

Write examples of herbivores carnivores and omnivo class 10 biology CBSE




