
The angular depression of the top and foot of a tower as seen from the top of a second tower which is 150m high and standing on the same level as the first are α and β respectively. If \[tan\alpha {\text{ }} = \dfrac{4}{3}\]and \[tan\beta = \dfrac{5}{2}\], the distance between their top is:
A.100m
B.120m
C.110m
D.130m
Answer
542.7k+ views
Hint: To find the distance between the tops of the tower firstly. We have to draw a rough diagram. Since, we have given the angle of depression. This means, the height of the second tower is more than the height of the first tower. Angle α is made to the first tower and β at the bottom of the tower.
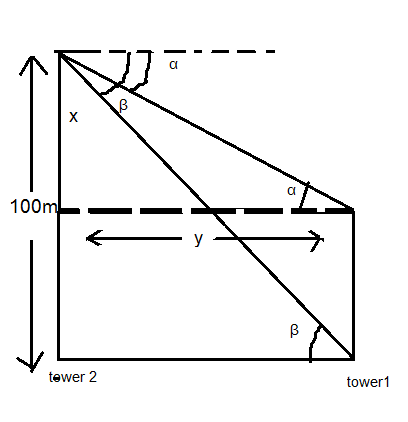
Complete step-by-step answer:
Now, ∠ FBD = ∠ BDE
This is because line BF is parallel to line DE and BD acts as transversal. The interior opposite angles formed by the transversal are equal.
∴ ∠ BDE = α
Similarly, ∠ FBC= ∠ BCA
Now, ABC formed is a triangle.
Let us consider that AC = y. here y is the distance between the towers. Also, height of tower 2 = AB = 150m.
Now in Δ ABC
$\tan \beta = \dfrac{{AB}}{{AC}} = \dfrac{{150}}{y}$
Also, we have given that $\tan \beta = \dfrac{5}{2}$
∴ $\dfrac{{150}}{y} = \dfrac{5}{2} \to y = \dfrac{{2 \times 150}}{5} = 60$
Y = 60m
Distance between the tower = 60m
Now in Δ BED, ∠ D=α and ∠ E = 90 degree
So, $\tan \alpha = \dfrac{{BE}}{{ED}}$. Also, we have given that $\tan \alpha = \dfrac{4}{3}$
Therefore $\dfrac{{BE}}{{ED}} = \dfrac{4}{3}$
Let us consider that BE = x
→ x is the height of tower 2 which is more than tower1.
Therefore $\dfrac{x}{{DE}} = \dfrac{4}{3}$
DE is also the distance between the two towers.
∴ DE= AC = y = 60m
Therefore $\dfrac{x}{{60}} = \dfrac{4}{3} \to x = \dfrac{{4 \times 60}}{3} = 80$
X= 80m
Now, distance between the two towers is given by BD.
∴ BDE is a right angled triangle.
Where BE is perpendicular, BD is hypotenuses and ED is base.
BY Pythagoras theorem,
${(hypotenuse)^2} = {(Base)^2} + {(perpendicular)^2}$
$\Rightarrow$ ${(BD)^2} = {(ED)^2} + {(BE)^2}$
$\Rightarrow$ ${(BD)^2} = {(y)^2} + {(x)^2}$
Putting values of x and y,
$\Rightarrow$ ${(BD)^2} = {(60)^2} + {(80)^2}$
$\Rightarrow$ ${(BD)^2} = 3600 + 6400$
$\Rightarrow$ ${(BD)^2} = 10000$
Take square root on both sides;
$
\Rightarrow (BD) = \sqrt {10000} \\
\Rightarrow BD = 100 \\
$
So, the distance between the top of the tower is 100m
Option (A) is correct.
Note: Angle of depression is a downward angle from the horizontal to the line of the sight from the observer to the same point of intersection.
Pythagoras theorem states that “ in a right angled triangle, the square of the hypotenuse side is equal to the sum of the squares of the other two sides of the triangle.
The tangent of an angle is equal to the side opposite to acute angle divided by the adjacent side of acute angle.

Complete step-by-step answer:
Now, ∠ FBD = ∠ BDE
This is because line BF is parallel to line DE and BD acts as transversal. The interior opposite angles formed by the transversal are equal.
∴ ∠ BDE = α
Similarly, ∠ FBC= ∠ BCA
Now, ABC formed is a triangle.
Let us consider that AC = y. here y is the distance between the towers. Also, height of tower 2 = AB = 150m.
Now in Δ ABC
$\tan \beta = \dfrac{{AB}}{{AC}} = \dfrac{{150}}{y}$
Also, we have given that $\tan \beta = \dfrac{5}{2}$
∴ $\dfrac{{150}}{y} = \dfrac{5}{2} \to y = \dfrac{{2 \times 150}}{5} = 60$
Y = 60m
Distance between the tower = 60m
Now in Δ BED, ∠ D=α and ∠ E = 90 degree
So, $\tan \alpha = \dfrac{{BE}}{{ED}}$. Also, we have given that $\tan \alpha = \dfrac{4}{3}$
Therefore $\dfrac{{BE}}{{ED}} = \dfrac{4}{3}$
Let us consider that BE = x
→ x is the height of tower 2 which is more than tower1.
Therefore $\dfrac{x}{{DE}} = \dfrac{4}{3}$
DE is also the distance between the two towers.
∴ DE= AC = y = 60m
Therefore $\dfrac{x}{{60}} = \dfrac{4}{3} \to x = \dfrac{{4 \times 60}}{3} = 80$
X= 80m
Now, distance between the two towers is given by BD.
∴ BDE is a right angled triangle.
Where BE is perpendicular, BD is hypotenuses and ED is base.
BY Pythagoras theorem,
${(hypotenuse)^2} = {(Base)^2} + {(perpendicular)^2}$
$\Rightarrow$ ${(BD)^2} = {(ED)^2} + {(BE)^2}$
$\Rightarrow$ ${(BD)^2} = {(y)^2} + {(x)^2}$
Putting values of x and y,
$\Rightarrow$ ${(BD)^2} = {(60)^2} + {(80)^2}$
$\Rightarrow$ ${(BD)^2} = 3600 + 6400$
$\Rightarrow$ ${(BD)^2} = 10000$
Take square root on both sides;
$
\Rightarrow (BD) = \sqrt {10000} \\
\Rightarrow BD = 100 \\
$
So, the distance between the top of the tower is 100m
Option (A) is correct.
Note: Angle of depression is a downward angle from the horizontal to the line of the sight from the observer to the same point of intersection.
Pythagoras theorem states that “ in a right angled triangle, the square of the hypotenuse side is equal to the sum of the squares of the other two sides of the triangle.
The tangent of an angle is equal to the side opposite to acute angle divided by the adjacent side of acute angle.
Recently Updated Pages
The height of a solid metal cylinder is 20cm Its r-class-10-maths-ICSE

If a train crossed a pole at a speed of 60kmhr in 30 class 10 physics CBSE

Name the Writs that the High Courts are empowered to class 10 social science CBSE

A tower is 5sqrt 3 meter high Find the angle of el-class-10-maths-CBSE

Immediate cause of variations of A Mutations B Environmental class 10 biology CBSE

A rectangular container whose base is a square of side class 10 maths CBSE

Trending doubts
Why is there a time difference of about 5 hours between class 10 social science CBSE

Why is Sardar Vallabhbhai Patel called the Iron man class 10 social science CBSE

Tropical deciduous trees shed their leaves in the dry class 10 social science CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

Write a letter to the principal requesting him to grant class 10 english CBSE

Leap year has days A 365 B 366 C 367 D 368 class 10 maths CBSE




