Question

What should be the angle between two plane mirrors, so that whatever be the angle of incident, the incident ray and the reflected ray from the two mirrors be parallel to each other?
$\left( A \right)\,60^\circ $
$\left( B \right)\,90^\circ $
$\left( C \right)\,120^\circ $
$\left( D \right)\,45^\circ $

Answer 1

Hint: First we should draw a diagram of two plane mirrors placed at an angle to each other. The diagram shows a ray incident on the second mirror after reflecting from the first mirror then after from that second mirror it reflects in such a way that the reflected ray is parallel to that of the incident ray .

Complete step by step solution:

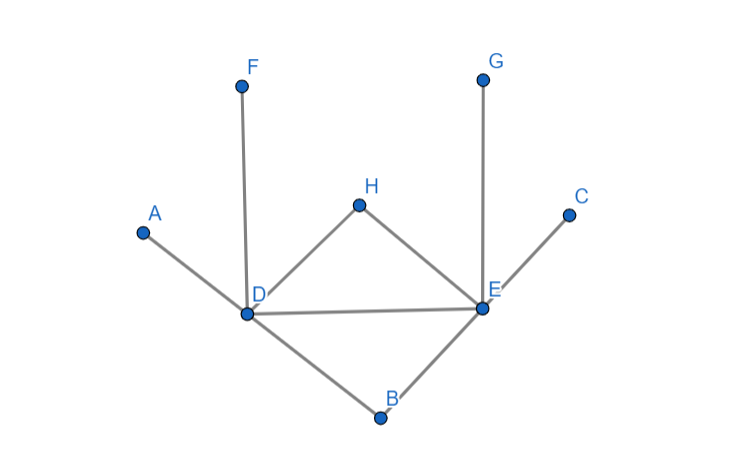
Here A and C are two mirrors where F and G are incident and reflected rays respectively. We need to find the $\angle DBE$.
Let DH bisects the $\angle FDE$ into two equals part let say it as ${\theta _1}$ $(\angle HDE = \angle FDH)$
Similarly EH bisects the $\angle DEG$ into two equal angle let say it as ${\theta _2}\left( {\angle DEH = \angle HEG} \right)$
Now we can say that
$\angle FDH = \angle HDE = {\theta _1}$
$\angle DEH = \angle HEG = {\theta _2}$
According to the question ray F and G are parallel to each other
Hence
$\angle FDE + \angle DEG = 180^\circ $
$ \Rightarrow 2{\theta _1} + 2{\theta _2} = 180^\circ $
$ \Rightarrow {\theta _1} + {\theta _2} = 90^\circ \cdot \cdot \cdot \cdot \left( {\dfrac{{180^\circ }}{2}} \right)$
We know the sum of all the angles in a triangle $ = 180^\circ $.
Hence in $\vartriangle DEH$ ,
$\angle HDB + \angle DEG + \angle EHD = 180^\circ $
$ \Rightarrow {\theta _1} + {\theta _2} + \angle EHD = 180^\circ $
We know that ${\theta _1} + {\theta _2} = 90^\circ $
$ \Rightarrow 90^\circ + \angle EHD = 180^\circ $
$ \Rightarrow \angle EHD = 90^\circ $
As we can see from the diagram that $DHBC$is a rhombus ,which says that the opposite angles are equal to each other.
That’s why
$\angle EHD = \angle DBE = 90^\circ (Ans)$
Therefore, the correct option is $\left( B \right)$ .

Note: If the correct diagram is not made then it becomes difficult to solve this kind of problem and while making the diagram make sure that the rays are exactly parallel to each other to get an accurate answer to this kind problem.