
Tangents are drawn to the circle \[{{x}^{2}}+{{y}^{2}}=12\] at the point where it met by the circle \[{{x}^{2}}+{{y}^{2}}-5x+3y-2=0;\] find the point of intersection of these tangents.
Answer
529.5k+ views
Hint:
The given equation of two circles are \[{{x}^{2}}+{{y}^{2}}=12\] (1) and \[{{x}^{2}}+{{y}^{2}}-5x+3y-2=0;\](2). We will find the equation of the common chord of the circle which we can assume as equation (3). Let this line meet the circle 1 (or 2) at A and B. let the tangents to circle 1 at A and B meet at P (a, b), then AB will be the chord of contact of a tangent to circle 1 from P, therefore, we will get the equation of AB (4). Now lines (3) and (4) are identical, now from equating the lines we get the point of intersection of the tangents.
Complete step by step answer:
We know that the given equation of circles is,
\[{{S}_{1}}={{x}^{2}}+{{y}^{2}}=12\]……….. (1)
\[{{S}_{2}}={{x}^{2}}+{{y}^{2}}-5x+3y-2=0;\]…….. (2)
We also know the equation of the common chord of the circles (1) and (2).
\[\begin{align}
& {{S}_{1}}-{{S}_{2}}=0 \\
& \Rightarrow {{x}^{2}}+{{y}^{2}}-12-{{x}^{2}}-{{y}^{2}}+5x-3y+2=0 \\
& \Rightarrow 5x-3y-10=0........(3) \\
\end{align}\].
Let this line meet circle 1 (or 2) at A and B.
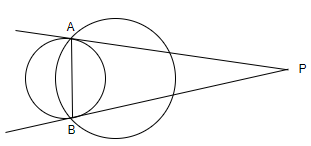
Let the tangents to circle 1 at A and B meet at P (a, b), then AB is the chord of contact of the tangent to circle 1 from P.
Therefore, we will get the equation of AB
\[xa+yb-12=0......(4)\]
Now the lines (3) and (4) are identical
\[\begin{align}
& \Rightarrow \dfrac{a}{b}=\dfrac{b}{-3}=\dfrac{-12}{-10} \\
& \Rightarrow \dfrac{b}{-3}=\dfrac{6}{5} \\
& \Rightarrow b=\dfrac{-18}{5} \\
& \Rightarrow a=6 \\
& \therefore a=6,b=\dfrac{-18}{5} \\
& \text{ P=}\left( \text{6,}\dfrac{-18}{5} \right) \\
\end{align}\]
Therefore, the point of intersection of tangent is \[\text{P=}\left( \text{6,}\dfrac{-18}{5} \right)\]
Note:
Another method
Here we are going to use the formula method
we know that the given two equation of circles are
\[{{S}_{1}}={{x}^{2}}+{{y}^{2}}=12\]
\[{{S}_{2}}={{x}^{2}}+{{y}^{2}}-5x+3y-2=0;\]
We know that the chord of intersection is
\[\begin{align}
& {{S}_{1}}-{{S}_{2}}=0 \\
& \Rightarrow {{x}^{2}}+{{y}^{2}}-12-{{x}^{2}}-{{y}^{2}}+5x-3y+2=0 \\
& \Rightarrow 5x-3y-10=0........(3) \\
\end{align}\]
Comparing equation (1) with the below equation, we get
\[\begin{align}
& lx+my+n=0 \\
& l=5,m=-3,n=-10 \\
\end{align}\]
We know that
Point of intersection of tangents as given in the concept = \[\left( \dfrac{-{{a}^{2}}l}{n},\dfrac{-{{a}^{2}}m}{n} \right)\]……... (2)
Here \[{{a}^{2}}=12\]
We already found the value of l, m, n. Substituting the value of l, m, n in (2)
Now we get,
\[\begin{align}
& \Rightarrow \left( \dfrac{-12\times 5}{-10},\dfrac{-12\times -3}{-10} \right) \\
& \Rightarrow \left( 6,\dfrac{-18}{5} \right) \\
\end{align}\]
Therefore, The point of intersection \[\text{P=}\left( \text{6,}\dfrac{-18}{5} \right)\]
The given equation of two circles are \[{{x}^{2}}+{{y}^{2}}=12\] (1) and \[{{x}^{2}}+{{y}^{2}}-5x+3y-2=0;\](2). We will find the equation of the common chord of the circle which we can assume as equation (3). Let this line meet the circle 1 (or 2) at A and B. let the tangents to circle 1 at A and B meet at P (a, b), then AB will be the chord of contact of a tangent to circle 1 from P, therefore, we will get the equation of AB (4). Now lines (3) and (4) are identical, now from equating the lines we get the point of intersection of the tangents.
Complete step by step answer:
We know that the given equation of circles is,
\[{{S}_{1}}={{x}^{2}}+{{y}^{2}}=12\]……….. (1)
\[{{S}_{2}}={{x}^{2}}+{{y}^{2}}-5x+3y-2=0;\]…….. (2)
We also know the equation of the common chord of the circles (1) and (2).
\[\begin{align}
& {{S}_{1}}-{{S}_{2}}=0 \\
& \Rightarrow {{x}^{2}}+{{y}^{2}}-12-{{x}^{2}}-{{y}^{2}}+5x-3y+2=0 \\
& \Rightarrow 5x-3y-10=0........(3) \\
\end{align}\].
Let this line meet circle 1 (or 2) at A and B.

Let the tangents to circle 1 at A and B meet at P (a, b), then AB is the chord of contact of the tangent to circle 1 from P.
Therefore, we will get the equation of AB
\[xa+yb-12=0......(4)\]
Now the lines (3) and (4) are identical
\[\begin{align}
& \Rightarrow \dfrac{a}{b}=\dfrac{b}{-3}=\dfrac{-12}{-10} \\
& \Rightarrow \dfrac{b}{-3}=\dfrac{6}{5} \\
& \Rightarrow b=\dfrac{-18}{5} \\
& \Rightarrow a=6 \\
& \therefore a=6,b=\dfrac{-18}{5} \\
& \text{ P=}\left( \text{6,}\dfrac{-18}{5} \right) \\
\end{align}\]
Therefore, the point of intersection of tangent is \[\text{P=}\left( \text{6,}\dfrac{-18}{5} \right)\]
Note:
Another method
Here we are going to use the formula method
we know that the given two equation of circles are
\[{{S}_{1}}={{x}^{2}}+{{y}^{2}}=12\]
\[{{S}_{2}}={{x}^{2}}+{{y}^{2}}-5x+3y-2=0;\]
We know that the chord of intersection is
\[\begin{align}
& {{S}_{1}}-{{S}_{2}}=0 \\
& \Rightarrow {{x}^{2}}+{{y}^{2}}-12-{{x}^{2}}-{{y}^{2}}+5x-3y+2=0 \\
& \Rightarrow 5x-3y-10=0........(3) \\
\end{align}\]
Comparing equation (1) with the below equation, we get
\[\begin{align}
& lx+my+n=0 \\
& l=5,m=-3,n=-10 \\
\end{align}\]
We know that
Point of intersection of tangents as given in the concept = \[\left( \dfrac{-{{a}^{2}}l}{n},\dfrac{-{{a}^{2}}m}{n} \right)\]……... (2)
Here \[{{a}^{2}}=12\]
We already found the value of l, m, n. Substituting the value of l, m, n in (2)
Now we get,
\[\begin{align}
& \Rightarrow \left( \dfrac{-12\times 5}{-10},\dfrac{-12\times -3}{-10} \right) \\
& \Rightarrow \left( 6,\dfrac{-18}{5} \right) \\
\end{align}\]
Therefore, The point of intersection \[\text{P=}\left( \text{6,}\dfrac{-18}{5} \right)\]
Recently Updated Pages
Are the points A 3 6 9 B 10 20 30 and C 25 41 5 the class 10 maths CBSE

Fungi are plants that lack class 10 biology CBSE

Explain how groundwater is recharged class 10 biology CBSE

What is 092 as a percent class 10 maths CBSE

In the given figure AOB and COD are two diameters of class 10 maths CBSE

The probability of India winning a test match against class 10 maths CBSE

Trending doubts
Write an application to the principal requesting five class 10 english CBSE

Why is there a time difference of about 5 hours between class 10 social science CBSE

Write a letter to the principal requesting him to grant class 10 english CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

What is the median of the first 10 natural numbers class 10 maths CBSE

Write examples of herbivores carnivores and omnivo class 10 biology CBSE




