
How do you solve and graph the compound inequality $ 2 < x <7 $ and $ 2x > 10 $ ?
Answer
464.1k+ views
Hint: We try to take points which have x coordinates that satisfies $ 2 < x < 7 $ and
$ 2x>10 $ . There is no restriction on the y coordinates. Based on the points we try to find the space or region in the 2-D plane which satisfies $ 2 < x < 7 $ and $ 2x>10 $ . We have two inequalities to solve to get the required interval.
Complete step by step solution:
Simplifying the inequation $ 2 < x < 7 $ , we get the interval of $ x\in \left( 2,7 \right) $ .
Now we solve the inequation $ 2 x > 10 $ .
We can solve the inequation treating them as equations for the operations like addition and subtraction. In case of multiplication and division we need to watch out for the negative values as that changes the inequality sign.
We divide both side of $ 2x>10 $ with positive number 2 and get
$ \begin{align}
& \dfrac{2x}{2}>\dfrac{10}{2} \\
& \Rightarrow x>5 \\
\end{align} $
The interval is $ x\in \left( 5,\infty \right) $ .
We need to take the combined result of $ x\in \left( 2,7 \right) $ and $ x\in \left( 5,\infty \right) $ .
The final solution gives $ x\in \left( 5,7 \right) $ .
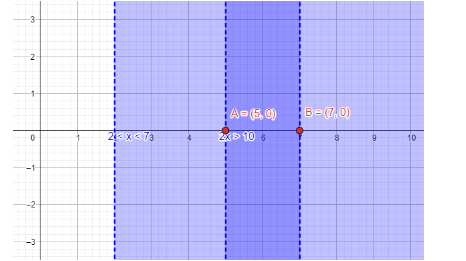
Note: We can also express the inequality as the interval system where $ 2x>10 $ defines that $ x>5 $ . The interval for the y coordinates will be anything which can be defined as $ y\in \left( -\infty ,\infty \right) $ . We also need to remember that the boundary points will not be considered as the solution for the inequations.
$ 2x>10 $ . There is no restriction on the y coordinates. Based on the points we try to find the space or region in the 2-D plane which satisfies $ 2 < x < 7 $ and $ 2x>10 $ . We have two inequalities to solve to get the required interval.
Complete step by step solution:
Simplifying the inequation $ 2 < x < 7 $ , we get the interval of $ x\in \left( 2,7 \right) $ .
Now we solve the inequation $ 2 x > 10 $ .
We can solve the inequation treating them as equations for the operations like addition and subtraction. In case of multiplication and division we need to watch out for the negative values as that changes the inequality sign.
We divide both side of $ 2x>10 $ with positive number 2 and get
$ \begin{align}
& \dfrac{2x}{2}>\dfrac{10}{2} \\
& \Rightarrow x>5 \\
\end{align} $
The interval is $ x\in \left( 5,\infty \right) $ .
We need to take the combined result of $ x\in \left( 2,7 \right) $ and $ x\in \left( 5,\infty \right) $ .
The final solution gives $ x\in \left( 5,7 \right) $ .

Note: We can also express the inequality as the interval system where $ 2x>10 $ defines that $ x>5 $ . The interval for the y coordinates will be anything which can be defined as $ y\in \left( -\infty ,\infty \right) $ . We also need to remember that the boundary points will not be considered as the solution for the inequations.
Recently Updated Pages
Master Class 12 Biology: Engaging Questions & Answers for Success

Master Class 12 Physics: Engaging Questions & Answers for Success

Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Trending doubts
How many ounces are in 500 mL class 8 maths CBSE

How many ten lakhs are in one crore-class-8-maths-CBSE

List some examples of Rabi and Kharif crops class 8 biology CBSE

In Indian rupees 1 trillion is equal to how many c class 8 maths CBSE

Name the states through which the Tropic of Cancer class 8 social science CBSE

When people say No pun intended what does that mea class 8 english CBSE





