
How do you solve and graph the compound inequality $2x + 5 \leqslant 11\;{\text{and}}\;4(x - 1) + 12 \geqslant 0?$
Answer
481.8k+ views
Hint: Solve the given inequalities for the value of $x$ then take the intersection of the solution. Now, to draw graphs, replace the inequalities with equality signs and draw graphs for the equations and shade the common region of both the graphs.
Complete step by step solution:
To solve and graph the compound inequality $2x + 5 \leqslant
11\;{\text{and}}\;4(x - 1) + 12 \geqslant 0$ we will first solve them separately for value of $x$ and then
take intersection of their solution
Solving first inequality:
$ \Rightarrow 2x + 5 \leqslant 11$
Subtracting $5$ from both sides,
\[
\Rightarrow 2x + 5 - 5 \leqslant 11 - 5 \\
\Rightarrow 2x \leqslant 6 \\
\]
Dividing both sides with $2$
$
\Rightarrow \dfrac{{2x}}{2} \leqslant \dfrac{6}{2} \\
\Rightarrow x \leqslant 3 \\
\therefore x \in \left( { - \infty ,\;3} \right] \\
$
Solving second inequality
$
\Rightarrow 4(x - 1) + 12 \geqslant 0 \\
\Rightarrow 4x - 4 + 12 \geqslant 0 \\
\Rightarrow 4x + 8 \geqslant 0 \\
$
Subtracting $8$ from both sides,
$
\Rightarrow 4x + 8 - 8 \geqslant 0 - 8 \\
\Rightarrow 4x \geqslant - 8 \\
$
Dividing both sides with $4$
$
\Rightarrow \dfrac{{4x}}{4} \geqslant \dfrac{{ - 8}}{4} \\
\Rightarrow x \geqslant - 2 \\
\therefore x \in \left[ { - 2,\;\infty } \right) \\
$
Now taking intersection of both the solutions, we will get
$
x \in \left[ { - 2,\;\infty } \right) \cap \left( { - \infty ,\;3} \right] \\
\Rightarrow x \in \left[ { - 2,\;3} \right] \\
$
So we get the compound solution of given inequalities as $x \in \left[ { - 2,\;3} \right]$
Now, to graph these inequalities, we will graph first graph the lines $x = - 2\;{\text{and}}\;x = 3$ as follows
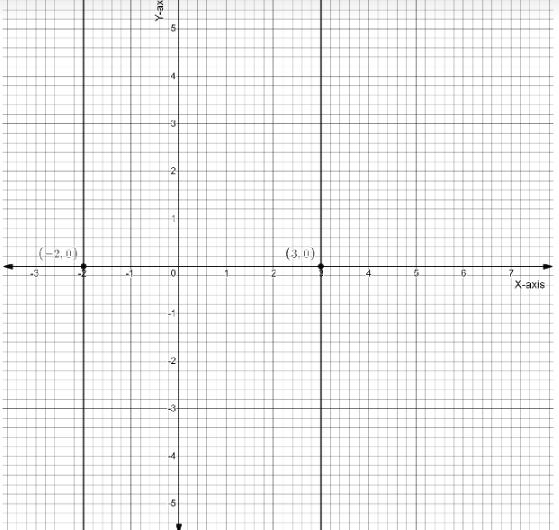
So this the graph of the lines $x = - 2\;{\text{and}}\;x = 3$, in order to draw the graph of the compound inequality whose solution is $x \in \left[ { - 2,\;3} \right]$ or we can also write it as $ - 2 \leqslant x \leqslant 3$ , we will shade portion between the two lines $x = - 2\;{\text{and}}\;x = 3$ and also since the given inequalities also includes $ - 2\;{\text{and}}\;3$ so we will left the line as it is and shade the portion in between them as follows

So this is the required graph for the given compound inequality.
Note: We have taken intersection of the solution of both equations because in the question it is given that $2x + 5 \leqslant 11\;{\text{and}}\;4(x - 1) + 12 \geqslant 0$, in which the word “and” in mathematics stands for the intersection operation and also for union operation, the word is “or”.
Complete step by step solution:
To solve and graph the compound inequality $2x + 5 \leqslant
11\;{\text{and}}\;4(x - 1) + 12 \geqslant 0$ we will first solve them separately for value of $x$ and then
take intersection of their solution
Solving first inequality:
$ \Rightarrow 2x + 5 \leqslant 11$
Subtracting $5$ from both sides,
\[
\Rightarrow 2x + 5 - 5 \leqslant 11 - 5 \\
\Rightarrow 2x \leqslant 6 \\
\]
Dividing both sides with $2$
$
\Rightarrow \dfrac{{2x}}{2} \leqslant \dfrac{6}{2} \\
\Rightarrow x \leqslant 3 \\
\therefore x \in \left( { - \infty ,\;3} \right] \\
$
Solving second inequality
$
\Rightarrow 4(x - 1) + 12 \geqslant 0 \\
\Rightarrow 4x - 4 + 12 \geqslant 0 \\
\Rightarrow 4x + 8 \geqslant 0 \\
$
Subtracting $8$ from both sides,
$
\Rightarrow 4x + 8 - 8 \geqslant 0 - 8 \\
\Rightarrow 4x \geqslant - 8 \\
$
Dividing both sides with $4$
$
\Rightarrow \dfrac{{4x}}{4} \geqslant \dfrac{{ - 8}}{4} \\
\Rightarrow x \geqslant - 2 \\
\therefore x \in \left[ { - 2,\;\infty } \right) \\
$
Now taking intersection of both the solutions, we will get
$
x \in \left[ { - 2,\;\infty } \right) \cap \left( { - \infty ,\;3} \right] \\
\Rightarrow x \in \left[ { - 2,\;3} \right] \\
$
So we get the compound solution of given inequalities as $x \in \left[ { - 2,\;3} \right]$
Now, to graph these inequalities, we will graph first graph the lines $x = - 2\;{\text{and}}\;x = 3$ as follows

So this the graph of the lines $x = - 2\;{\text{and}}\;x = 3$, in order to draw the graph of the compound inequality whose solution is $x \in \left[ { - 2,\;3} \right]$ or we can also write it as $ - 2 \leqslant x \leqslant 3$ , we will shade portion between the two lines $x = - 2\;{\text{and}}\;x = 3$ and also since the given inequalities also includes $ - 2\;{\text{and}}\;3$ so we will left the line as it is and shade the portion in between them as follows

So this is the required graph for the given compound inequality.
Note: We have taken intersection of the solution of both equations because in the question it is given that $2x + 5 \leqslant 11\;{\text{and}}\;4(x - 1) + 12 \geqslant 0$, in which the word “and” in mathematics stands for the intersection operation and also for union operation, the word is “or”.
Recently Updated Pages
Master Class 10 English: Engaging Questions & Answers for Success

Master Class 10 Social Science: Engaging Questions & Answers for Success

Master Class 10 Maths: Engaging Questions & Answers for Success

Master Class 10 Science: Engaging Questions & Answers for Success

Class 10 Question and Answer - Your Ultimate Solutions Guide

Master Class 12 Biology: Engaging Questions & Answers for Success

Trending doubts
Why is there a time difference of about 5 hours between class 10 social science CBSE

The aviation fuel used in the engines of jet airplanes class 10 physics CBSE

What is the scientific name of apple class 10 biology CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

Fill the blanks with proper collective nouns 1 A of class 10 english CBSE

Write examples of herbivores carnivores and omnivo class 10 biology CBSE




