Question

PQRS is a square. If \[PQ = 10cm\] then \[PR = ........cm\].
A). \[10\]
B). \[20\]
C). \[10\sqrt 2 \]
D). \[2\sqrt {10} \]

Answer 1

Hint: The length of one side of a square is given. We know that all four sides of a square will have the same length. Here we have to find the diagonal of the square. A diagonal of a square can split the square into two right-angled triangles where the diagonal will be the hypotenuse so using the Pythagoras theorem, we can find the length of the diagonal.
Formula:
Pythagoras theorem: \[A{C^2} = A{B^2} + B{C^2}\] where \[ABC\] is a right-angled triangle \[\left( \angle{B} \right) = {90^o} \].
And some other formulas that we need to know:
1.\[\sqrt {{x^2}} = x\]
2.\[\sqrt {ab} = \sqrt a \times \sqrt b \]
3.\[\sqrt a \times \sqrt a = a\]

Complete step-by-step solution:
It is given that \[PQRS\] is a square with \[PQ = 10cm\]. We know that all the sides of the square will have the same length.

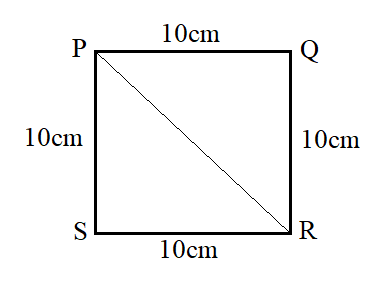
Therefore \[QR = 10cm, RS = 10cm\] & \[SP = 10cm\].
We aim to find the length of \[PR\] which is the diagonal of a square\[PQRS\].
By Pythagoras theorem, we know that for a right-angled triangle \[\Delta ABC\],\[A{C^2} = A{B^2} + B{C^2}\] that is hypotenuse square is equal to the sum of an opposite square and adjacent square. From the diagram, let us take the right-angled triangle\[\Delta PSR\].
So, for the right-angled triangle \[\Delta PSR\] we have \[P{R^2} = P{S^2} + S{R^2}\].
We know that \[\left( \angle{S} \right) = {90^o},SR = 10cm\] & \[PS = 10cm\].
Substituting these values in \[P{R^2} = P{S^2} + S{R^2}\]we get
\[P{R^2} = {10^2} + {10^{^2}}\]
Simplifying this we get
\[P{R^2} = 100 + 100\]
On simplifying this we get
\[P{R^2} = 200\]
But we need the value for \[PR\] so let us take the square root
\[\sqrt {P{R^2}} = \sqrt {200} \]
Now let us write \[200\] in terms of its factors
\[\sqrt {P{R^2}} = \sqrt {20 \times 10} \]
Now let us write \[20\] in terms of its factors
\[\sqrt {P{R^2}} = \sqrt 2 \times \sqrt {10} \times \sqrt {10} \]
Let us split the square root using the formula, \[\sqrt {ab} = \sqrt a \times \sqrt b \]
\[\sqrt {P{R^2}} = \sqrt 2 \times \sqrt {10} \times \sqrt {10} \]
Noe using the formula \[\sqrt a \times \sqrt a = a\] we get
\[\sqrt {P{R^2}} = \sqrt 2 \times 10\]
\[\sqrt {P{R^2}} = 10\sqrt 2 \]
Again, using the formula \[\sqrt {{x^2}} = x\] we get
\[PR = 10\sqrt 2 \]
Therefore, the length of the diagonal of the square \[PQRS\] is \[PR = 10\sqrt 2 cm\].
Now let us see the options, option (a) \[10\] cannot be the right answer since we got the length of \[PR\] as \[10\sqrt 2 cm\].
Option (b) \[20\] cannot be the right answer since we got the length of \[PR\] as \[10\sqrt 2 cm\] from the above calculation.
Option (c) \[10\sqrt 2 \] is the right answer since we got the length of \[PR\] as \[10\sqrt 2 cm\] from the above calculation.
Option (d) \[2\sqrt {10} \] cannot be the right answer since we got the length of \[PR\] as \[10\sqrt 2 cm\] from the above calculation.
Thus, option (c) \[10\sqrt 2 \] is the correct answer.

Note: We can also take another right-angled triangle that is \[\Delta PQR\]and use the Pythagoras theorem to find the length of the diagonal \[PR\], we will get the same answer as we got above. This is because all the sides of the square take the same length.