
How many lines of symmetry does a circle have?
(a) 1
(b) 2
(c) 3
(d) infinite
Answer
583.8k+ views
Hint: The definition of the lines of symmetry would be the hint here. The lines of symmetry are the lines which divide the shape they pass through into two equal parts.
Complete step-by-step answer:
So a regular polygon of n sides will have 2n lines of symmetry since the line through every vertex can divide it into two equal parts. So a regular hexagon will have 12 lines of symmetry, a regular heptagon will have 14 lines of symmetry, a regular octagon will have 16 lines of symmetry, a regular icosagon will have 40 lines of symmetry and so on.
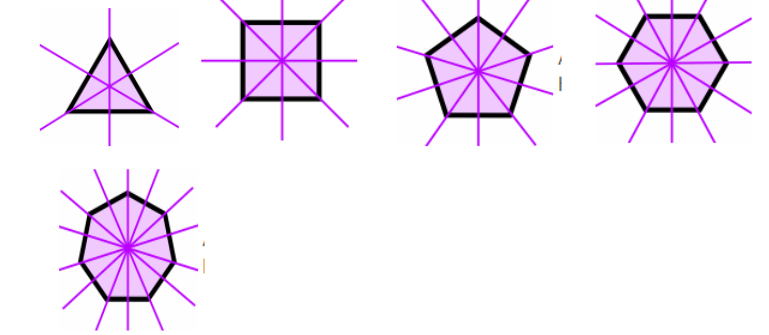
As we can see from the above figures, the number of the lines of symmetry vary with the number of sides the polygon has.
Now let us come to the case of the circle. It does not have any sides which cannot be distinctly shown.
Actually it has an infinite number of sides. That is the reason the surface line of the circle, more accurately the circumference or the perimeter of the circle looks smooth and without any corner points.
So as we learnt earlier the number of lines of symmetry vary as 2n if the number of sides of the polygon are n.
But the circle has an infinite number of sides. So it should have infinitely many lines of symmetry.
So the option(d) is the correct one.
Note: Alternatively, the lines of symmetry can be defined as the lines which when drawn perpendicular to any side of the polygon will pass through the centre of the polygon. But in a circle a line drawn at any angle will always pass through the centre. Thus for a circle an infinite number of lines will satisfy the equation. Thus the lines of symmetry for a circle are infinite.
Complete step-by-step answer:
So a regular polygon of n sides will have 2n lines of symmetry since the line through every vertex can divide it into two equal parts. So a regular hexagon will have 12 lines of symmetry, a regular heptagon will have 14 lines of symmetry, a regular octagon will have 16 lines of symmetry, a regular icosagon will have 40 lines of symmetry and so on.

As we can see from the above figures, the number of the lines of symmetry vary with the number of sides the polygon has.
Now let us come to the case of the circle. It does not have any sides which cannot be distinctly shown.
Actually it has an infinite number of sides. That is the reason the surface line of the circle, more accurately the circumference or the perimeter of the circle looks smooth and without any corner points.
So as we learnt earlier the number of lines of symmetry vary as 2n if the number of sides of the polygon are n.
But the circle has an infinite number of sides. So it should have infinitely many lines of symmetry.
So the option(d) is the correct one.
Note: Alternatively, the lines of symmetry can be defined as the lines which when drawn perpendicular to any side of the polygon will pass through the centre of the polygon. But in a circle a line drawn at any angle will always pass through the centre. Thus for a circle an infinite number of lines will satisfy the equation. Thus the lines of symmetry for a circle are infinite.
Recently Updated Pages
The height of a solid metal cylinder is 20cm Its r-class-10-maths-ICSE

If a train crossed a pole at a speed of 60kmhr in 30 class 10 physics CBSE

Name the Writs that the High Courts are empowered to class 10 social science CBSE

A tower is 5sqrt 3 meter high Find the angle of el-class-10-maths-CBSE

Immediate cause of variations of A Mutations B Environmental class 10 biology CBSE

A rectangular container whose base is a square of side class 10 maths CBSE

Trending doubts
Why is there a time difference of about 5 hours between class 10 social science CBSE

Tropical deciduous trees shed their leaves in the dry class 10 social science CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

Write a letter to the principal requesting him to grant class 10 english CBSE

The uses of bleaching powder are A It is used bleaching class 10 chemistry CBSE

Leap year has days A 365 B 366 C 367 D 368 class 10 maths CBSE




