Question

Let $U$ be the universal set and $A \cup B \cup C = U$. Then $\left\{ {\left( {A - B} \right) \cup \left( {B - C} \right) \cup \left( {C - A} \right)} \right\}'$ is equal to
A.$A \cup B \cup C$
B.$A \cup \left( {B \cap C} \right)$
C.$A \cap B \cap C$
D.$A \cap \left( {B \cup C} \right)$

Answer 1

Hint: In order to find the value of $\left\{ {\left( {A - B} \right) \cup \left( {B - C} \right) \cup \left( {C - A} \right)} \right\}'$, initiate with the drawing the Venn diagram of sets separately like for $\left( {A - B} \right)$, $\left( {B - C} \right)$ and $\left( {C - A} \right)$, find their union and then complement them. Complement will represent the part which is not covered by the unions. And, we will get the required results.

Complete answer:
We are given with three sets: A, B and C. And, some set equations are given, so we will use Venn diagrams to solve for $\left\{ {\left( {A - B} \right) \cup \left( {B - C} \right) \cup \left( {C - A} \right)} \right\}'$.
So, basically, we are given with $A \cup B \cup C = U$. Means all the elements of the sets combine to form the Universal set, which in diagram is represented as:

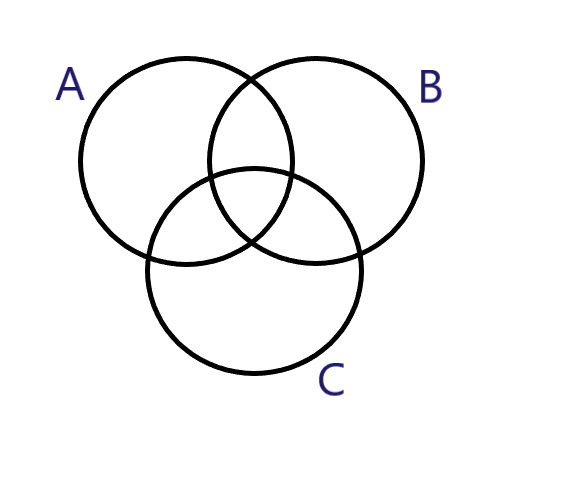
Now, we would start with finding the values separately in $\left\{ {\left( {A - B} \right) \cup \left( {B - C} \right) \cup \left( {C - A} \right)} \right\}'$,.
Starting with $\left( {A - B} \right)$. Basically, $\left( {A - B} \right)$ it depicts the region which has all A elements except the portion which has B elements, represented as:

The Yellow portion shows $\left( {A - B} \right)$.
Now, for $\left( {B - C} \right)$, the Area’s which covers all elements of B but not C.
The pink color represents that:

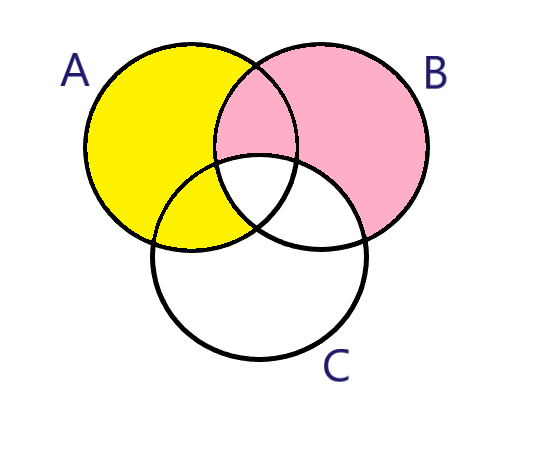
And, it gives $\left( {A - B} \right) \cup \left( {B - C} \right)$.
Now, for $\left( {C - A} \right)$.
The Area which has all elements of C but not the elements of A. Represented as green color:

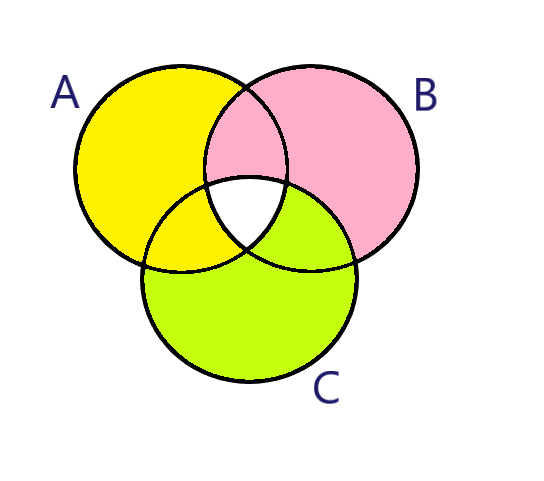
And, now it gives \[\left\{ {\left( {A - B} \right) \cup \left( {B - C} \right) \cup \left( {C - A} \right)} \right\}\].
But we need the complement of the value. Complement means the portion which are in Universal set but not in \[\left\{ {\left( {A - B} \right) \cup \left( {B - C} \right) \cup \left( {C - A} \right)} \right\}\].
So, the portion becomes:
\[\left\{ {\left( {A - B} \right) \cup \left( {B - C} \right) \cup \left( {C - A} \right)} \right\}' = U - \left\{ {\left( {A - B} \right) \cup \left( {B - C} \right) \cup \left( {C - A} \right)} \right\}\]
And, in the above diagram it is the white portion in the middle, which shows that. And, the portion is \[A \cap B \cap C\], the intersection of the three sets.
Therefore, $\left\{ {\left( {A - B} \right) \cup \left( {B - C} \right) \cup \left( {C - A} \right)} \right\}'$ is equal to \[A \cap B \cap C\].
Therefore, option (C) is the correct answer.

Note:
-Universal sets are always represented by capital U. And, complement is represented with a single quote, for example: A’ is the complement of A.
-Venn Diagram is the best method to find the intersection and union of sets. So, it is always preferred to use Venn diagrams.