
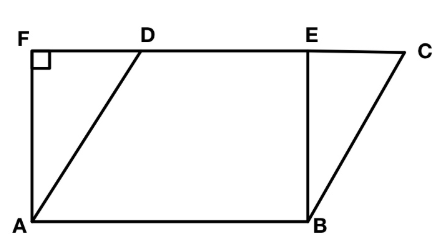
In the given figure, if parallelogram ABCD and rectangle ABEF are equal area then:
A. Perimeter of ABCD =Perimeter of ABEF
B. Perimeter of ABCD < Perimeter of ABEF
C. Perimeter of ABCD>Perimeter of ABEF
D. Perimeter of ABCD=$$\dfrac{1}{2} \times$$(Perimeter of ABEF)

Answer
579.3k+ views
Hint: In this question it is given that if a parallelogram ABCD and rectangle ABEF are equal in area then we have to find the relation between the perimeter of ABCD and the perimeter of ABEF.
So to find the relation between their perimeters we first need to find the relation between their corresponding sides.
Complete step-by-step answer:
As we know that the opposite sides of a rectangle and as well as parallelogram are equal.
So we can write, for rectangle ABEF
AB=EF………(1)
AF=BE……....(2)
And for a parallelogram ABCD,
AB=CD……….(3)
AD=BC…….....(4)
Since rectangle ABEF and parallelogram ABCD have the same base AB and have equal areas,
So from equation (1) and (3) we can write,
CD=EF…….(5)
In $\triangle ADF$, $$\angle AFD=90$$
Which implies,$\triangle ADF$ forming a right angle.
So for an right angle triangle hypotenuse > perpendicular
So we can write AD>AF……..(6)
Similarly, for $\triangle BCE$
BC>BE……….(7)
Now we add (6) and (7)
AD+BC>AF+BE
Or, AB+AD+BC>AB+AF+BE [adding AB in the both side]
Or, AB+AD+BC+CD>AB+AF+BE+EF [ since, EF=CD]
It can be written as,
AB+BC+CD+DA>AB+BE+EF+FA [since AD=DA and AF=FA].......(8)
Now as we know that,
Perimeter of a parallelogram ABCD=AB+BC+CD+DA
And perimeter of a rectangle ABEF=AB+BE+EF+FA
So from (8) we can write,
Perimeter of ABCD>Perimeter of ABEF
So the correct option is option C.
Note: To solve this type of question you need to have the basic idea about perimeter and how to measure the perimeter of a rectangle and parallelogram, i.e, the summation of all the sides. Also one more concept is that while adding two inequalities we have to add the left side of one inequation with the left side of the other inequation and similarly in right side also , like we did with the inequations (6) and (7).
So to find the relation between their perimeters we first need to find the relation between their corresponding sides.
Complete step-by-step answer:
As we know that the opposite sides of a rectangle and as well as parallelogram are equal.
So we can write, for rectangle ABEF
AB=EF………(1)
AF=BE……....(2)
And for a parallelogram ABCD,
AB=CD……….(3)
AD=BC…….....(4)
Since rectangle ABEF and parallelogram ABCD have the same base AB and have equal areas,
So from equation (1) and (3) we can write,
CD=EF…….(5)
In $\triangle ADF$, $$\angle AFD=90$$
Which implies,$\triangle ADF$ forming a right angle.
So for an right angle triangle hypotenuse > perpendicular
So we can write AD>AF……..(6)
Similarly, for $\triangle BCE$
BC>BE……….(7)
Now we add (6) and (7)
AD+BC>AF+BE
Or, AB+AD+BC>AB+AF+BE [adding AB in the both side]
Or, AB+AD+BC+CD>AB+AF+BE+EF [ since, EF=CD]
It can be written as,
AB+BC+CD+DA>AB+BE+EF+FA [since AD=DA and AF=FA].......(8)
Now as we know that,
Perimeter of a parallelogram ABCD=AB+BC+CD+DA
And perimeter of a rectangle ABEF=AB+BE+EF+FA
So from (8) we can write,
Perimeter of ABCD>Perimeter of ABEF
So the correct option is option C.
Note: To solve this type of question you need to have the basic idea about perimeter and how to measure the perimeter of a rectangle and parallelogram, i.e, the summation of all the sides. Also one more concept is that while adding two inequalities we have to add the left side of one inequation with the left side of the other inequation and similarly in right side also , like we did with the inequations (6) and (7).
Recently Updated Pages
How do you convert r6sec theta into Cartesian form class 10 maths CBSE

How do you solve dfrac5y3dfracy+72y6+1 and find any class 10 maths CBSE

If sin A+B1 and cos AB1 0circ le left A+B rightle 90circ class 10 maths CBSE

On the number line 10 is to the of zero class 10 maths CBSE

How do you solve 5xge 30 class 10 maths CBSE

In the following sentence supply a verb in agreement class 10 english CBSE

Trending doubts
Write an application to the principal requesting five class 10 english CBSE

Why is there a time difference of about 5 hours between class 10 social science CBSE

List of Lok Sabha Speakers of India

Which one of the following is the deepest seaport of class 10 social science CBSE

Write a letter to the principal requesting him to grant class 10 english CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths




