
In the given figure, chord AB is the diameter of the circle. What is the measure of the $\angle BDC$ ?
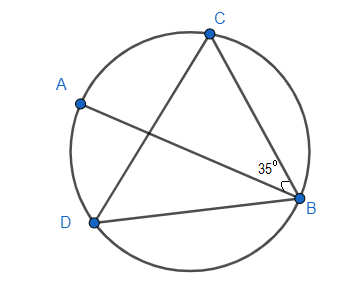

Answer
577.2k+ views
Hint: For solving the question, you need to use the property that the angles subtended by the same segment of the circle are equal, and the angle subtended by a diameter of the circle at the circumference is equal to $90{}^\circ $.
Complete step-by-step solution -
Let’s start by drawing a diagram with all the required constructions for our better visualisation.
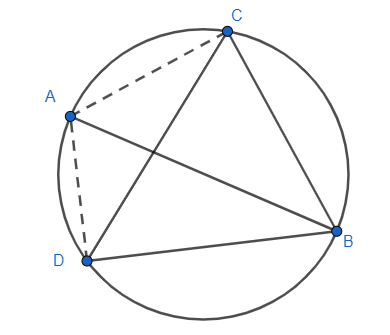
Now we know that the angles subtended by the same segment of the circle are equal and $\angle ABC\text{ and }\angle \text{ADC}$ are angles subtended by the same segment AC.
$\therefore \angle ABC=\angle ADC$
It is given in the question that $\angle ABC=15{}^\circ $ . If we combine this with above result, we get
$\angle ABC=\angle ADC=15{}^\circ $
Now from the figure, we can see that $\angle ADB$ can be written as the sum of $\angle ADC\text{ and }\angle BDC$ . We also found that $\angle ADC=15{}^\circ $ . So, we can say:
$\angle BDC+\angle ADC=\angle ADB$
$\Rightarrow \angle BDC+15{}^\circ =\angle ADB$
Now, as it is given that AB is the diameter of the circle and we know angle subtended by a diameter of the circle at the circumference is equal to $90{}^\circ $ . So, we can say that $\angle ADB=90{}^\circ $ .
$\therefore \angle BDC+15{}^\circ =90{}^\circ $
$\Rightarrow \angle BDC=75{}^\circ $
Therefore, the measure of the $\angle BDC$ is equal to $75{}^\circ $ .
Note: It is prescribed to learn all the basic theorems related to circles as they are regularly used in the questions related to circles and cyclic quadrilaterals, as we did in the above question.
Complete step-by-step solution -
Let’s start by drawing a diagram with all the required constructions for our better visualisation.

Now we know that the angles subtended by the same segment of the circle are equal and $\angle ABC\text{ and }\angle \text{ADC}$ are angles subtended by the same segment AC.
$\therefore \angle ABC=\angle ADC$
It is given in the question that $\angle ABC=15{}^\circ $ . If we combine this with above result, we get
$\angle ABC=\angle ADC=15{}^\circ $
Now from the figure, we can see that $\angle ADB$ can be written as the sum of $\angle ADC\text{ and }\angle BDC$ . We also found that $\angle ADC=15{}^\circ $ . So, we can say:
$\angle BDC+\angle ADC=\angle ADB$
$\Rightarrow \angle BDC+15{}^\circ =\angle ADB$
Now, as it is given that AB is the diameter of the circle and we know angle subtended by a diameter of the circle at the circumference is equal to $90{}^\circ $ . So, we can say that $\angle ADB=90{}^\circ $ .
$\therefore \angle BDC+15{}^\circ =90{}^\circ $
$\Rightarrow \angle BDC=75{}^\circ $
Therefore, the measure of the $\angle BDC$ is equal to $75{}^\circ $ .
Note: It is prescribed to learn all the basic theorems related to circles as they are regularly used in the questions related to circles and cyclic quadrilaterals, as we did in the above question.
Recently Updated Pages
The height of a solid metal cylinder is 20cm Its r-class-10-maths-ICSE

If a train crossed a pole at a speed of 60kmhr in 30 class 10 physics CBSE

Name the Writs that the High Courts are empowered to class 10 social science CBSE

A tower is 5sqrt 3 meter high Find the angle of el-class-10-maths-CBSE

Immediate cause of variations of A Mutations B Environmental class 10 biology CBSE

A rectangular container whose base is a square of side class 10 maths CBSE

Trending doubts
Write an application to the principal requesting five class 10 english CBSE

Why is there a time difference of about 5 hours between class 10 social science CBSE

Write a letter to the principal requesting him to grant class 10 english CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

What is the median of the first 10 natural numbers class 10 maths CBSE

Write examples of herbivores carnivores and omnivo class 10 biology CBSE




