
In the electric field due to a point charge q, a test charge is carried from A to the points B, C, D and E lying on the same circle around q. The work done is
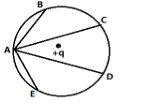
A. The least along AB
B. The least along AD
C. Zero along any one of the paths AB, AD, AC and AE
D. The least along AE.

Answer
526.5k+ views
Hint: Work done in moving a test charge (the magnitude of the test charge is considered to be negligible or very small) through some path, under the influence of the other point charge will the difference in the potential created at the points due to that point charge.
Complete answer:
The point charge which is situated inside the circle will produce some potential at each point on the circumference of the given circle but we have to deal with the potential which will be generated at the point A. So now we will write the expression for the potential generated at the point A due to the point charge $q$.
So the potential created at point $A$ due to point charge $q$, that is ${U_A} = \dfrac{{Kq}}{r}$
Where $q = $point charge, $K = $electrostatic constant, $r = $radius of the circle(since the distance between the point charge,$q$ and the point A will be the same as that of the value of the radius of the circle.)
Now similarly the potential due to this point charge at points B, C, D, and E will be the same, since the value of the point charge is same for each point and the value of the distance from the point charge and the given points is the same that is equal to the radius of the given circle.
So, the potential at given points,
$ = {U_B} = {U_C} = {U_D} = {U_E} = \dfrac{{Kq}}{r}$
Hence the work done in moving the charge from point A to point B will be the difference between the potentials at the both points.
So, the work done in moving the charge from point A to point B,
${W_{AB}} = {U_A} - {U_B} = \dfrac{{Kq}}{r} - \dfrac{{Kq}}{r} = 0$
Similarly
${W_{AC}} = {U_A} - {U_C} = \dfrac{{Kq}}{r} - \dfrac{{Kq}}{r} = 0$
${W_{AD}} = {U_A} - {U_D} = \dfrac{{Kq}}{r} - \dfrac{{Kq}}{r} = 0$
And ${W_{AE}} = {U_A} - {U_E} = \dfrac{{Kq}}{r} - \dfrac{{Kq}}{r} = 0$
Hence, we see that the work done in moving the charge from point A to point B, C, D and E is zero.
So, the correct answer is “Option C”.
Note:
Here the point charge creates an electric field about its area of influence. So, the work will be done on moving a charge through any electric field and this work done will be proportional to the amount of the charge moved and they will also be proportional to the difference of the potential in the starting and the potential in the final position. This is similar to the work done in the area of the gravitational attraction.
Complete answer:
The point charge which is situated inside the circle will produce some potential at each point on the circumference of the given circle but we have to deal with the potential which will be generated at the point A. So now we will write the expression for the potential generated at the point A due to the point charge $q$.
So the potential created at point $A$ due to point charge $q$, that is ${U_A} = \dfrac{{Kq}}{r}$
Where $q = $point charge, $K = $electrostatic constant, $r = $radius of the circle(since the distance between the point charge,$q$ and the point A will be the same as that of the value of the radius of the circle.)
Now similarly the potential due to this point charge at points B, C, D, and E will be the same, since the value of the point charge is same for each point and the value of the distance from the point charge and the given points is the same that is equal to the radius of the given circle.
So, the potential at given points,
$ = {U_B} = {U_C} = {U_D} = {U_E} = \dfrac{{Kq}}{r}$
Hence the work done in moving the charge from point A to point B will be the difference between the potentials at the both points.
So, the work done in moving the charge from point A to point B,
${W_{AB}} = {U_A} - {U_B} = \dfrac{{Kq}}{r} - \dfrac{{Kq}}{r} = 0$
Similarly
${W_{AC}} = {U_A} - {U_C} = \dfrac{{Kq}}{r} - \dfrac{{Kq}}{r} = 0$
${W_{AD}} = {U_A} - {U_D} = \dfrac{{Kq}}{r} - \dfrac{{Kq}}{r} = 0$
And ${W_{AE}} = {U_A} - {U_E} = \dfrac{{Kq}}{r} - \dfrac{{Kq}}{r} = 0$
Hence, we see that the work done in moving the charge from point A to point B, C, D and E is zero.
So, the correct answer is “Option C”.
Note:
Here the point charge creates an electric field about its area of influence. So, the work will be done on moving a charge through any electric field and this work done will be proportional to the amount of the charge moved and they will also be proportional to the difference of the potential in the starting and the potential in the final position. This is similar to the work done in the area of the gravitational attraction.
Recently Updated Pages
Physics and Measurement Mock Test 2025 – Practice Questions & Answers

NCERT Solutions For Class 5 English Marigold - The Little Bully

NCERT Solutions For Class 12 Maths Three Dimensional Geometry Exercise 11.1

NCERT Solutions For Class 11 English Woven Words (Poem) - Ajamil And The Tigers

NCERT Solutions For Class 6 Hindi Durva - Bhaaloo

NCERT Solutions For Class 12 Physics In Hindi - Wave Optics

Trending doubts
Which are the Top 10 Largest Countries of the World?

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE

Why is the cell called the structural and functional class 12 biology CBSE

a Tabulate the differences in the characteristics of class 12 chemistry CBSE

Who discovered the cell and how class 12 biology CBSE

Draw a labelled sketch of the human eye class 12 physics CBSE




