Question

In the adjoining figure DP is parallel to AC, then the ratio of area of the triangle PCB and quadrilateral ABCD is

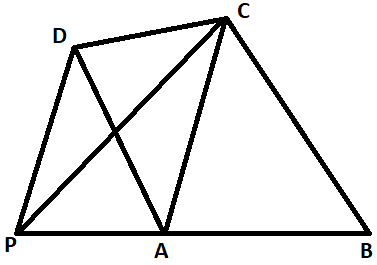
A. $1:1$
B. $1:2$
C. $1:4$
D. $2:3$

Answer 1

Hint: While solving such kinds of problems, we have to know about some properties of triangles. First property is that the triangles drawn between two parallel lines with the same base have equal areas. The second property is that the ratio of areas of triangles with equal height is equal to the ratio of their bases, as the area of a triangle is the half of product of base and height.

Step-By-Step answer:
Here the quadrilateral PACD is a trapezium, as there is one pair of parallel lines in the quadrilateral.
Now the first property of the triangle is very important and crucial as we are going to use this property of the triangles here.
The first property says that the triangles drawn between two parallel lines with the same base have equal areas.
So any two triangles which are drawn in between the parallel lines with a common base, then the areas of these two triangles are equal.
Now consider the triangle PCB, as shown in the above figure, it has two triangles in it which are as given below:
$ \Rightarrow \Delta PCB = \Delta PCA + \Delta ACB$
Now consider the quadrilateral ABCD, as shown in the above figure, it has two triangles in it which are as given below:
\[ \Rightarrow ABCD = \Delta DCA + \Delta ACB\]
Both the polygons, the triangle PCB and the quadrilateral have a common triangle which is \[\Delta ACB\].
Now consider the triangles $\Delta PCA$ and \[\Delta DCA\].
Observe carefully from the figure, here the two triangles $\Delta PCA$ and \[\Delta DCA\] are in between the parallel lines DP and CA, and these two triangles have a common base AC, which means that the areas of these two triangles are equal.
$ \Rightarrow Area(\Delta PCA) = Area(\Delta DCA)$
$\therefore \Delta PCA = \Delta DCA$
As considered before the triangle \[\Delta PCB\] and the quadrilateral $ABCD$, as given below:
$ \Rightarrow \Delta PCB = \Delta PCA + \Delta ACB$
\[ \Rightarrow ABCD = \Delta DCA + \Delta ACB\]
$\because \Delta PCA = \Delta DCA$
Substituting the above expression in the expressions of the obtained triangle PCB and the quadrilateral ABCD, as given below:
$ \Rightarrow \Delta PCB = \Delta DCA + \Delta ACB$ and
\[ \Rightarrow ABCD = \Delta DCA + \Delta ACB\]
$ \Rightarrow \Delta PCB = ABCD$
$\therefore Area(\Delta PCB) = Area(ABCD)$
Hence $\dfrac{{Area(\Delta PCB)}}{{Area(ABCD)}} = 1$

The ratio of area of the triangle PCB and quadrilateral ABCD is $1:1$.

Note: Here while solving this problem the one thing we have to keep in mind is that the first and foremost important property of triangles, if any two triangles are in between the two parallel lines sharing a common base then the two triangles have equal areas, remember here that the two triangles need not share only base, but it can be any common side of the two triangles, then the areas of the two triangles are still equal. The property still holds true.