Question

In an isosceles triangle, the circumcentre, the incentre, the orthocentre and the centroid are-
A. Collinear
B. Coincide
C. Do not coincide
D. None of the above

Answer 1

Hint: The knowledge of different centres of a triangle will be used in this problem. We will begin by constructing an isosceles triangle, and make a perpendicular from one vertex to the opposite side, which is the one having a different length from the other two. We will then check if the circumcentre, the incentre, the orthocentre and the centroid lie on that line or not. If they do, we will check if they coincide or not.

Complete step-by-step answer:
We need to find the relationship between the four centres of a triangle, which are the circumcentre, the incentre, the orthocentre and the centroid.
(a)The centroid is the point of intersection of the three medians. A median is the line joining a vertex to the midpoint of the opposite side.
(b)The orthocentre is the point of intersection of the three altitudes. An altitude is the line joining a vertex and the opposite side, such that it is perpendicular to that opposite side.
(c)The incentre is the point of intersection of the three angle bisectors. An angle bisector is the line joining the vertex and the opposite side such that it divides the angle made at the vertex in two equal halves.
(d)The circumcentre is the point of intersection of the perpendicular bisector of each side. A perpendicular bisector is a line perpendicular to a given line, and passing through its centre. It need not pass through the opposite vertex of the triangle.

We will now construct an arbitrary isosceles triangle ABC with an altitude through the non-equal side at D as-

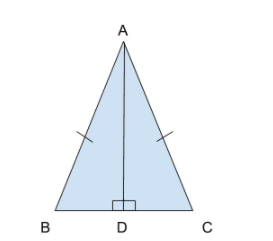
We can see that AD is an altitude of the isosceles triangle ABC with AB = AC. This means that the orthocentre lies on the line AD.
Now, we will consider the two right-angled triangle ADB and ADC-
$\begin{align}
  &In\;\vartriangle ADB\;and\vartriangle ADC, \\
  &AD = AD\left( {common} \right) \\
  &AB = AC\left( {isosceles\;triangle} \right) \\
  &\angle ADB = \angle ADC\left( {right - angled} \right) \\
  &By\;RHS\;congruency - \\
  &\vartriangle ADB\; \cong \vartriangle ADC \\
\end{align} $
Triangle ADB and ADC are congruent, so by apply the property of corresponding parts of congruent triangles, we can write that-
BD = DC
$\angle BAD = \angle CAD$
Using these equations, we can deduce that-
AD is the altitude due to our initial assumption, hence the orthocentre lies on AD.
AD is the median because it divides BC in two equal halves(BD = DC), hence the centroid lies on AD.
AD is the angular bisector because it divides $\angle {\text{A}}$ in two equal halves($\angle BAD = \angle CAD$), hence the incentive lies on AD.
AD is the perpendicular bisector of BC, because it is perpendicular to it, and divides it in two equal halves as well(BD = DC), hence the circumcentre lies on AD.

These four conditions show us that all the centres lie on the same line AD. But we cannot prove that they coincide, because they coincide only when the triangle is equilateral. Hence, the correct option is A.

Note: An important point to note here is that the altitude must be drawn only through the non-equal side, which is BC in this case. This enables us to bring symmetricity in the figure and we can prove the two triangles congruent. Also, the students must thoroughly remember the properties of all the four centres and how they are constructed. This answer can be used as a general result by the students in other problems.