
In an isosceles triangle ABC, with AB = AC, the bisectors of $\angle B{\text{ and }}\angle {\text{C}}$ intersect each other at O. Join A to O. Show that : OB = OC
Answer
570.3k+ views
Hint: In this particular type of question we have to proceed by using the property of angle bisector at point B and C and then using the triangle property that angles opposite to equal sides of a triangle are equal and its converse is also true .
Complete step-by-step solution -
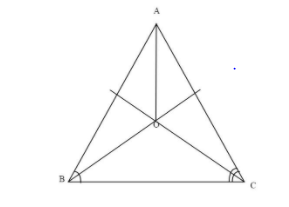
$\vartriangle ABC$ is an isosceles with AB = AC,
$\therefore \angle B = \angle C$
[ Since , angles opposite to equal sides are equal ]
$ \Rightarrow \dfrac{1}{2}\angle B = \dfrac{1}{2}\angle C$ [Divide both sides by 2]
$\begin{gathered}
\Rightarrow \angle OBC = \angle OCB \\
And{\text{ }}\angle {\text{OBA = }}\angle OCA \\
\end{gathered} $ [Angle bisectors]
$ \Rightarrow OB = OC$ [Side opposite to the equal angles are equal]
Note: Remember to recall the properties of triangle bisectors while solving this particular type of questions . Also constructing a diagram helps to get a clear picture of what we need to find out . Note that Angle Bisector Theorem says that an angle bisector of a triangle will divide the opposite side into two segments that are proportional to the other two sides of the triangle but the Angle Bisector Theorem Converse states that if a point is in the interior of an angle and equidistant from the sides, then it lies on the bisector of that angle .
Complete step-by-step solution -

$\vartriangle ABC$ is an isosceles with AB = AC,
$\therefore \angle B = \angle C$
[ Since , angles opposite to equal sides are equal ]
$ \Rightarrow \dfrac{1}{2}\angle B = \dfrac{1}{2}\angle C$ [Divide both sides by 2]
$\begin{gathered}
\Rightarrow \angle OBC = \angle OCB \\
And{\text{ }}\angle {\text{OBA = }}\angle OCA \\
\end{gathered} $ [Angle bisectors]
$ \Rightarrow OB = OC$ [Side opposite to the equal angles are equal]
Note: Remember to recall the properties of triangle bisectors while solving this particular type of questions . Also constructing a diagram helps to get a clear picture of what we need to find out . Note that Angle Bisector Theorem says that an angle bisector of a triangle will divide the opposite side into two segments that are proportional to the other two sides of the triangle but the Angle Bisector Theorem Converse states that if a point is in the interior of an angle and equidistant from the sides, then it lies on the bisector of that angle .
Recently Updated Pages
The height of a solid metal cylinder is 20cm Its r-class-10-maths-ICSE

If a train crossed a pole at a speed of 60kmhr in 30 class 10 physics CBSE

Name the Writs that the High Courts are empowered to class 10 social science CBSE

A tower is 5sqrt 3 meter high Find the angle of el-class-10-maths-CBSE

Immediate cause of variations of A Mutations B Environmental class 10 biology CBSE

A rectangular container whose base is a square of side class 10 maths CBSE

Trending doubts
Why is there a time difference of about 5 hours between class 10 social science CBSE

Why is Sardar Vallabhbhai Patel called the Iron man class 10 social science CBSE

Tropical deciduous trees shed their leaves in the dry class 10 social science CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

Write a letter to the principal requesting him to grant class 10 english CBSE

Leap year has days A 365 B 366 C 367 D 368 class 10 maths CBSE




