
In a rectangle ABCD, the coordinates of A and B are $ \left( 1,2 \right) $ and $ \left( 3,6 \right) $ respectively and some diameter of the circumscribing circle of ABCD has equation $ 2x-y+4=0 $ . Then the area of the rectangle is. \[\]
A.16\[\]
B. $ 2\sqrt{10} $ \[\]
C. $ 2\sqrt{5} $ \[\]
D.20\[\]
Answer
534k+ views
Hint: We need to find the distance formula \[\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}}\] between two points to find the length of the side AB. We now need to find the length of BC to find the area. We find the slope of AB $ \dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}} $ and check whether the diameter line $ 2x-y+4=0 $ is parallel to AB or BC. If the diameter line is parallel to AB, we find the distance of B from the that line using distance formula of a line $ ax+by+c=0 $ from a point $ \left( {{x}_{1}},{{y}_{1}} \right) $ as $ \dfrac{a{{x}_{1}}+b{{y}_{1}}+c}{\sqrt{{{a}^{2}}+{{b}^{2}}}} $ . We take twice the distance to get BC. We find the area $ AB\cdot BC $ .\[\]
Complete step by step answer:
We are given that in a rectangle ABCD, the coordinates of A and B are $ \left( 1,2 \right) $ and $ \left( 3,6 \right) $ respectively. We use the distance formula between two points and the length of side AB as
\[AB=\sqrt{{{\left( 3-1 \right)}^{2}}+{{\left( 6-2 \right)}^{2}}}=\sqrt{{{2}^{2}}+{{4}^{2}}}=\sqrt{20}=4\sqrt{5}\]
We know that the diagonals in a rectangle bisect each other and hence the point of intersection of diagonals and centre of the circumscribing circle will coincide. So the diameter which passes through the centre will be parallel to at least length or the breadth of the rectangle. \[\]
We are given that the equation of the diameter line is $ 2x-y+4=0 $ . We know the slope of the line in the form $ ax+by+c=0 $ is $ \dfrac{-a}{b} $ . So the slope of the diameter line is $ -\left( \dfrac{2}{-1} \right)=2 $ . The slope of the line joining $ A\left( 1,2 \right) $ and $ B\left( 3,6 \right) $ in two point form is $ \dfrac{6-2}{3-1}=\dfrac{4}{2}=2 $ . Since slopes of diameter and AB are the same, they are parallel. Let us denote the points of intersection of diameter line $ 2x-y+4=0 $ with AD and BC as E and F respectively. We have the rough diagram as;\[\]
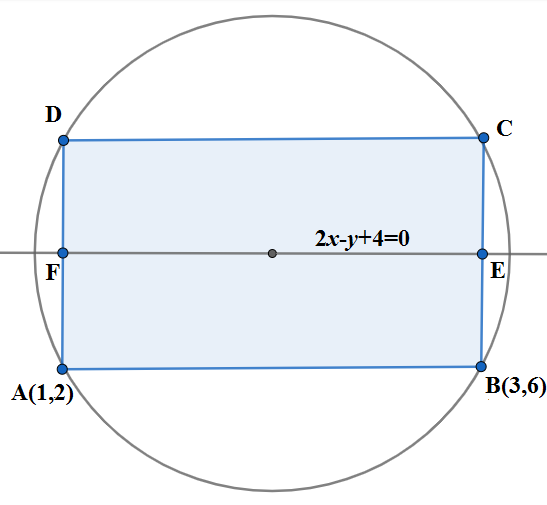
We see that of the side BC is twice BE. We find BE using the point to line distance formula with point $ B\left( 3,6 \right) $ and line $ 2x-y+4=0 $ as
\[BE=\dfrac{2\left( 3 \right)-6+4}{\sqrt{{{2}^{2}}+{{\left( - 1\right)}^{2}}}}=\dfrac{4}{\sqrt{5}}\]
So the length of BC is
\[BC=2BE=2\times \dfrac{4}{\sqrt{5}}=\dfrac{8}{\sqrt{5}}\]
So the area of rectangle ABCD is
\[\text{Area}=AB\cdot BC=2\sqrt{5}\cdot \dfrac{8}{\sqrt{5}}=16\]
Hence the correct option is A.
Note:
We can alternatively find AE finding the distance between parallel lines AB and $ 2x-y+4=0 $ . We can find the equation of AB in two point form that is $ y-{{y}_{1}}=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}\left( x-{{x}_{1}} \right) $ . We find the distance between two lines $ ax+by+{{c}_{1}}=0 $ and $ ax+by+{{c}_{2}}=0 $ as $ \dfrac{\left| {{c}_{1}}-{{c}_{2}} \right|}{\sqrt{{{a}^{2}}+{{b}^{2}}}} $ . We also note that the diameter line is also bisecting the sides AD and BC. If the diameter would have been perpendicular to BC we have to find all equations of sides and equations of circle and then the coordinates of vertices C and D.
Complete step by step answer:
We are given that in a rectangle ABCD, the coordinates of A and B are $ \left( 1,2 \right) $ and $ \left( 3,6 \right) $ respectively. We use the distance formula between two points and the length of side AB as
\[AB=\sqrt{{{\left( 3-1 \right)}^{2}}+{{\left( 6-2 \right)}^{2}}}=\sqrt{{{2}^{2}}+{{4}^{2}}}=\sqrt{20}=4\sqrt{5}\]
We know that the diagonals in a rectangle bisect each other and hence the point of intersection of diagonals and centre of the circumscribing circle will coincide. So the diameter which passes through the centre will be parallel to at least length or the breadth of the rectangle. \[\]
We are given that the equation of the diameter line is $ 2x-y+4=0 $ . We know the slope of the line in the form $ ax+by+c=0 $ is $ \dfrac{-a}{b} $ . So the slope of the diameter line is $ -\left( \dfrac{2}{-1} \right)=2 $ . The slope of the line joining $ A\left( 1,2 \right) $ and $ B\left( 3,6 \right) $ in two point form is $ \dfrac{6-2}{3-1}=\dfrac{4}{2}=2 $ . Since slopes of diameter and AB are the same, they are parallel. Let us denote the points of intersection of diameter line $ 2x-y+4=0 $ with AD and BC as E and F respectively. We have the rough diagram as;\[\]

We see that of the side BC is twice BE. We find BE using the point to line distance formula with point $ B\left( 3,6 \right) $ and line $ 2x-y+4=0 $ as
\[BE=\dfrac{2\left( 3 \right)-6+4}{\sqrt{{{2}^{2}}+{{\left( - 1\right)}^{2}}}}=\dfrac{4}{\sqrt{5}}\]
So the length of BC is
\[BC=2BE=2\times \dfrac{4}{\sqrt{5}}=\dfrac{8}{\sqrt{5}}\]
So the area of rectangle ABCD is
\[\text{Area}=AB\cdot BC=2\sqrt{5}\cdot \dfrac{8}{\sqrt{5}}=16\]
Hence the correct option is A.
Note:
We can alternatively find AE finding the distance between parallel lines AB and $ 2x-y+4=0 $ . We can find the equation of AB in two point form that is $ y-{{y}_{1}}=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}\left( x-{{x}_{1}} \right) $ . We find the distance between two lines $ ax+by+{{c}_{1}}=0 $ and $ ax+by+{{c}_{2}}=0 $ as $ \dfrac{\left| {{c}_{1}}-{{c}_{2}} \right|}{\sqrt{{{a}^{2}}+{{b}^{2}}}} $ . We also note that the diameter line is also bisecting the sides AD and BC. If the diameter would have been perpendicular to BC we have to find all equations of sides and equations of circle and then the coordinates of vertices C and D.
Recently Updated Pages
How do you write an algebraic expression of product class 10 maths CBSE

How do you find all rational roots for x42x38x2+10 class 10 maths CBSE

What kind of compound would be least likely to dissolve class 10 chemistry CBSE

If alpha beta gamma are the lengths of the altitudes class 10 maths CBSE

Choose the option which best expresses the meaning class 10 chemistry CBSE

Identify the category to which the underlined adjective class 10 english CBSE

Trending doubts
Write an application to the principal requesting five class 10 english CBSE

Why is there a time difference of about 5 hours between class 10 social science CBSE

Write a letter to the principal requesting him to grant class 10 english CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

What is the median of the first 10 natural numbers class 10 maths CBSE

Write examples of herbivores carnivores and omnivo class 10 biology CBSE




