
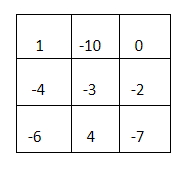
In a magic square, each row, each column, each diagonal have the same sum. Check if this is a magic square.

Answer
580.8k+ views
Hint: Here we have a grid filled with integers. We check if the sum of elements of every row is equal to sum of elements of every column and equal to sum of elements of every diagonal. If all the sums are equal to the same constant, we say it is a magic square.
* A magic square of order \[n\] is an arrangement of \[{n^2}\] distinct numbers such that sum of \[n\] numbers in every row, sum of \[n\] numbers in every column and sum of \[n\] numbers in every diagonal sum to the same constant.
Complete step by step solution:
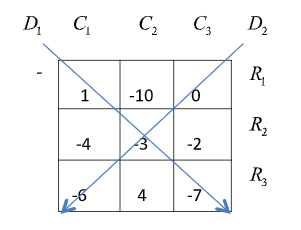
To solve the magic square we allot names to all rows, all columns and both diagonals to make calculations easier.
Say, the first row is denoted by \[{R_1}\] , second row by \[{R_2}\] and third row by \[{R_3}\].
Similarly, first column is denoted by \[{C_1}\] , second column by \[{C_2}\] and third column by \[{C_3}\]
Diagonal from top left to bottom right be denoted by \[{D_1}\] and diagonal from top right to left bottom by \[{D_2}\]
Elements of \[{R_1}\] are \[1, - 10,0\]
Therefore, sum of elements of \[{R_1}\] is \[(1) + ( - 10) + (0) = 1 - 10 = - 9\]
Elements of \[{R_2}\] are \[ - 4, - 3, - 2\]
Therefore, sum of elements of \[{R_2}\] is \[( - 4) + ( - 3) + ( - 2) = - (4 + 3 + 2) = - 9\]
Elements of \[{R_3}\] are \[ - 6,4, - 7\]
Therefore, sum of elements of \[{R_3}\] is \[( - 6) + (4) + ( - 7) = 4 - (6 + 7) = 4 - 13 = - 9\]
Elements of \[{C_1}\] are \[1, - 4, - 6\]
Therefore, sum of elements of \[{C_1}\] is \[(1) + ( - 4) + ( - 6) = 1 - (6 + 4) = 1 - 10 = - 9\]
Elements of \[{C_2}\] are \[ - 10, - 3,4\]
Therefore, sum of elements of \[{C_2}\] is \[( - 10) + ( - 3) + (4) = 4 - (10 + 3) = 4 - 13 = - 9\]
Elements of \[{C_3}\] are \[0, - 2, - 7\]
Therefore, sum of elements of \[{C_3}\] is \[(0) + ( - 2) + ( - 7) = - (2 + 7) = - 9\]
Elements of \[{D_1}\] are \[1, - 3, - 7\]
Therefore, sum of elements of \[{D_1}\] is \[(1) + ( - 3) + ( - 7) = 1 - (3 + 7) = 1 - 10 = - 9\]
Elements of \[{D_2}\] are \[0, - 3, - 6\]
Therefore, sum of elements of \[{D_2}\] is \[(0) + ( - 3) + ( - 6) = - (3 + 6) = - 9\]
Clearly sum or elements of each row is \[ - 9\].
Sum of elements of each column is \[ - 9\] .
And the sum of elements of each diagonal is \[ - 9\] .
Since, numbers in each row, numbers in each column and numbers in each diagonal sum up to the same constant i.e. \[ - 9\]
Therefore this arrangement of numbers in the form of a grid is a magic square.
Note:
Students should be aware of the meaning of terms ‘Rows’ and ‘Columns’ as it can create confusion sometimes. A Row is the horizontal data arrangement and a column is the vertical data arrangement.
* Generally, a magic square has all elements as positive distinct numbers, then constant sum is called ‘Magic constant’ or ‘Magic sum’ and is denoted by \[M\] and is calculated by the formula \[M = \dfrac{{n({n^2} + 1)}}{2}\], where \[n\] is the order of the square.
* A magic square of order \[n\] is an arrangement of \[{n^2}\] distinct numbers such that sum of \[n\] numbers in every row, sum of \[n\] numbers in every column and sum of \[n\] numbers in every diagonal sum to the same constant.
Complete step by step solution:
To solve the magic square we allot names to all rows, all columns and both diagonals to make calculations easier.
Say, the first row is denoted by \[{R_1}\] , second row by \[{R_2}\] and third row by \[{R_3}\].
Similarly, first column is denoted by \[{C_1}\] , second column by \[{C_2}\] and third column by \[{C_3}\]
Diagonal from top left to bottom right be denoted by \[{D_1}\] and diagonal from top right to left bottom by \[{D_2}\]

Elements of \[{R_1}\] are \[1, - 10,0\]
Therefore, sum of elements of \[{R_1}\] is \[(1) + ( - 10) + (0) = 1 - 10 = - 9\]
Elements of \[{R_2}\] are \[ - 4, - 3, - 2\]
Therefore, sum of elements of \[{R_2}\] is \[( - 4) + ( - 3) + ( - 2) = - (4 + 3 + 2) = - 9\]
Elements of \[{R_3}\] are \[ - 6,4, - 7\]
Therefore, sum of elements of \[{R_3}\] is \[( - 6) + (4) + ( - 7) = 4 - (6 + 7) = 4 - 13 = - 9\]
Elements of \[{C_1}\] are \[1, - 4, - 6\]
Therefore, sum of elements of \[{C_1}\] is \[(1) + ( - 4) + ( - 6) = 1 - (6 + 4) = 1 - 10 = - 9\]
Elements of \[{C_2}\] are \[ - 10, - 3,4\]
Therefore, sum of elements of \[{C_2}\] is \[( - 10) + ( - 3) + (4) = 4 - (10 + 3) = 4 - 13 = - 9\]
Elements of \[{C_3}\] are \[0, - 2, - 7\]
Therefore, sum of elements of \[{C_3}\] is \[(0) + ( - 2) + ( - 7) = - (2 + 7) = - 9\]
Elements of \[{D_1}\] are \[1, - 3, - 7\]
Therefore, sum of elements of \[{D_1}\] is \[(1) + ( - 3) + ( - 7) = 1 - (3 + 7) = 1 - 10 = - 9\]
Elements of \[{D_2}\] are \[0, - 3, - 6\]
Therefore, sum of elements of \[{D_2}\] is \[(0) + ( - 3) + ( - 6) = - (3 + 6) = - 9\]
Clearly sum or elements of each row is \[ - 9\].
Sum of elements of each column is \[ - 9\] .
And the sum of elements of each diagonal is \[ - 9\] .
Since, numbers in each row, numbers in each column and numbers in each diagonal sum up to the same constant i.e. \[ - 9\]
Therefore this arrangement of numbers in the form of a grid is a magic square.
Note:
Students should be aware of the meaning of terms ‘Rows’ and ‘Columns’ as it can create confusion sometimes. A Row is the horizontal data arrangement and a column is the vertical data arrangement.
* Generally, a magic square has all elements as positive distinct numbers, then constant sum is called ‘Magic constant’ or ‘Magic sum’ and is denoted by \[M\] and is calculated by the formula \[M = \dfrac{{n({n^2} + 1)}}{2}\], where \[n\] is the order of the square.
Recently Updated Pages
You are awaiting your class 10th results Meanwhile class 7 english CBSE

Master Class 7 Social Science: Engaging Questions & Answers for Success

Master Class 7 Science: Engaging Questions & Answers for Success

Class 7 Question and Answer - Your Ultimate Solutions Guide

Master Class 7 English: Engaging Questions & Answers for Success

Master Class 7 Maths: Engaging Questions & Answers for Success

Trending doubts
Convert 200 Million dollars in rupees class 7 maths CBSE

Full Form of IASDMIPSIFSIRSPOLICE class 7 social science CBSE

i What trees does Mr Wonka mention Which tree does class 7 english CBSE

What are the controls affecting the climate of Ind class 7 social science CBSE

Write a letter to the editor of the national daily class 7 english CBSE

Welcome speech for Christmas day celebration class 7 english CBSE





