
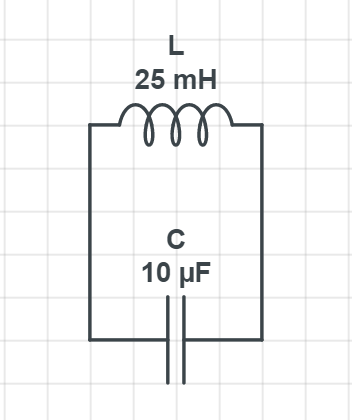
If maximum energy is stored in a capacitor at $t=0$ then find the time after which current in the circuit will be maximum.
\[\begin{align}
& A.\dfrac{\pi }{2}ms \\
& B.\dfrac{\pi }{4}ms \\
& C.\pi ms \\
& D.2ms \\
\end{align}\]

Answer
508.2k+ views
Hint: In a LCR circuit, the inductor $L$, capacitance $C$ and resistance $R$ are connected to a AC source. Here the LCR is connected in series circuit; it can also be connected in parallel circuit. Then the phase difference between the current and the voltage is $\theta$ generally.
Formula used:
$T=2\pi\sqrt{LC}$
Complete step by step answer:
We know that the source of an AC circuit is sinusoidal. Then there is a phase difference between the voltage and current. If the phase difference between the current and voltage is zero, then both are said to be in phase, and if the phase difference is not equal to zero, then both are said to be out of phase. Resonance is a special condition, which is observed when RLC is connected in series; here there is no phase difference between the current and the voltage.
We know that the frequency of the circuit is given as,$\omega=\dfrac{1}{\sqrt{LC}}$
$\implies T=2\pi\sqrt{LC}$, where $T$ is the time-period of one cycle.
Here, we have LC circuit, and given that, $L=25mH$ and $C=10\mu F$, substituting the values, we get,
$T=2\pi\sqrt{25\times 10^{-3}\times 10\times 10^{-6}}$
$\implies T=2\pi\sqrt{25\times 10^{-8}}$
$\implies T=2\pi\times 5\times 10^{-4}$
$\therefore T=\pi\times 10^{-3}s$
Since the AC is sinusoidal in nature and the time-period of the wave is $T=\pi\times 10^{-3}s$, we know that at $\dfrac{T}{4}$, the capacitance discharges the charge stored in it, and thus the current is maximum. Hence at $T_{max}=\dfrac{T}{4}=\dfrac{\pi\times 10^{-3}}{4}$
$\therefore T_{max}=\dfrac{\pi}{4}ms$
So, the correct answer is “Option B”.
Note:
$Z$ is the impedance of the circuit or the total resistance offered by the circuit, it is given as $Z=\sqrt{R^{2}+(X_{L}-X_{C})^{2}}$. Here $X_{L},X_{C}$ are the inductive reactance and the capacitive reactance. Using the frequency of the circuit, we can solve this sum.
Formula used:
$T=2\pi\sqrt{LC}$
Complete step by step answer:
We know that the source of an AC circuit is sinusoidal. Then there is a phase difference between the voltage and current. If the phase difference between the current and voltage is zero, then both are said to be in phase, and if the phase difference is not equal to zero, then both are said to be out of phase. Resonance is a special condition, which is observed when RLC is connected in series; here there is no phase difference between the current and the voltage.
We know that the frequency of the circuit is given as,$\omega=\dfrac{1}{\sqrt{LC}}$
$\implies T=2\pi\sqrt{LC}$, where $T$ is the time-period of one cycle.
Here, we have LC circuit, and given that, $L=25mH$ and $C=10\mu F$, substituting the values, we get,
$T=2\pi\sqrt{25\times 10^{-3}\times 10\times 10^{-6}}$
$\implies T=2\pi\sqrt{25\times 10^{-8}}$
$\implies T=2\pi\times 5\times 10^{-4}$
$\therefore T=\pi\times 10^{-3}s$
Since the AC is sinusoidal in nature and the time-period of the wave is $T=\pi\times 10^{-3}s$, we know that at $\dfrac{T}{4}$, the capacitance discharges the charge stored in it, and thus the current is maximum. Hence at $T_{max}=\dfrac{T}{4}=\dfrac{\pi\times 10^{-3}}{4}$
$\therefore T_{max}=\dfrac{\pi}{4}ms$
So, the correct answer is “Option B”.
Note:
$Z$ is the impedance of the circuit or the total resistance offered by the circuit, it is given as $Z=\sqrt{R^{2}+(X_{L}-X_{C})^{2}}$. Here $X_{L},X_{C}$ are the inductive reactance and the capacitive reactance. Using the frequency of the circuit, we can solve this sum.
Recently Updated Pages
Master Class 10 English: Engaging Questions & Answers for Success

Master Class 10 Social Science: Engaging Questions & Answers for Success

Master Class 10 Maths: Engaging Questions & Answers for Success

Master Class 10 Science: Engaging Questions & Answers for Success

Class 10 Question and Answer - Your Ultimate Solutions Guide

Master Class 12 Biology: Engaging Questions & Answers for Success

Trending doubts
Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE

Which are the Top 10 Largest Countries of the World?

Why is the cell called the structural and functional class 12 biology CBSE

a Tabulate the differences in the characteristics of class 12 chemistry CBSE

Pomato is a Somatic hybrid b Allopolyploid c Natural class 12 biology CBSE

Who discovered the cell and how class 12 biology CBSE




