
Identify whether the given pair of angles are either complementary angles or supplementary angles:
\[{100^ \circ },{80^ \circ }\]
Answer
564.3k+ views
Hint: Complementary angle: Two angles are said to be a complement to each other if their sum is\[{90^ \circ }\]. That is if $a^\circ + b^\circ = 90^\circ $ then we call the angles a and b as complementary angles.
Supplementary angle: Similarly, when the sum of two angles is equal to \[{180^ \circ }.\] We call them supplementary angles. That is when $a^\circ + b^\circ = 180^\circ $ then the angles a and b are known as supplementary angles.
Complete step by step answer:
Let us consider the two given angles are \[{100^ \circ },{80^ \circ }\]. To find whether they are complementary or supplementary angles we know we have to find the sum of these two given angles.
If the sum is \[{90^ \circ }\], then the given angles are complementary and if the sum is \[{180^ \circ }\], then the given angles are supplementary.
Let us calculate the sum of the angles.
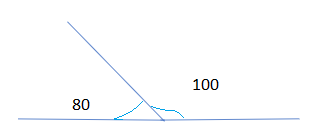
Here, the sum of the given two angles is \[{100^ \circ } + {80^ \circ } = {180^ \circ }\]The sum of the given angles is \[{180^ \circ }\].
Hence by the definition of the supplementary angles, we can conclude that the two angles are supplementary.
Hence, we have identified that the given pair of angles are supplementary angles as their sum is \[{180^ \circ }\].
Additional information: If two angles are supplementary and they have one common side and a common vertex, we can call them adjacent angles. In the above given diagram \[{100^ \circ },{80^ \circ }\] are adjacent angles and A is the adjacent vertex. Moreover, the other two sides of these angles will form a straight line.
Note:
To solve these type questions easily, we have to remember that the addition of the given angles is either $a^\circ + b^\circ = 90^\circ $or $a^\circ + b^\circ = 180^\circ $. From the result of the addition, we call the angle is the complementary angle or supplementary angle.
Supplementary angle: Similarly, when the sum of two angles is equal to \[{180^ \circ }.\] We call them supplementary angles. That is when $a^\circ + b^\circ = 180^\circ $ then the angles a and b are known as supplementary angles.
Complete step by step answer:
Let us consider the two given angles are \[{100^ \circ },{80^ \circ }\]. To find whether they are complementary or supplementary angles we know we have to find the sum of these two given angles.
If the sum is \[{90^ \circ }\], then the given angles are complementary and if the sum is \[{180^ \circ }\], then the given angles are supplementary.
Let us calculate the sum of the angles.

Here, the sum of the given two angles is \[{100^ \circ } + {80^ \circ } = {180^ \circ }\]The sum of the given angles is \[{180^ \circ }\].
Hence by the definition of the supplementary angles, we can conclude that the two angles are supplementary.
Hence, we have identified that the given pair of angles are supplementary angles as their sum is \[{180^ \circ }\].
Additional information: If two angles are supplementary and they have one common side and a common vertex, we can call them adjacent angles. In the above given diagram \[{100^ \circ },{80^ \circ }\] are adjacent angles and A is the adjacent vertex. Moreover, the other two sides of these angles will form a straight line.
Note:
To solve these type questions easily, we have to remember that the addition of the given angles is either $a^\circ + b^\circ = 90^\circ $or $a^\circ + b^\circ = 180^\circ $. From the result of the addition, we call the angle is the complementary angle or supplementary angle.
Recently Updated Pages
The element which has the strongest metallic bond among class 10 chemistry CBSE

Prove the following statement cot 4A+cot 2Acsc 4Acsc class 10 maths CBSE

There are 6 multiple choice questions in an examination class 10 maths CBSE

In xylem fibre gives strength to A Vessels B Tracheids class 10 biology CBSE

Fill in the blank with the most appropriate word He class 10 english CBSE

The Sum of the roots of the following equations is class 10 maths CBSE

Trending doubts
Write an application to the principal requesting five class 10 english CBSE

Why is there a time difference of about 5 hours between class 10 social science CBSE

Write a letter to the principal requesting him to grant class 10 english CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

What is the median of the first 10 natural numbers class 10 maths CBSE

Write examples of herbivores carnivores and omnivo class 10 biology CBSE




