
How do you graph the function \[f(x) = - 4x\] ?
Answer
475.2k+ views
Hint:We need to draw the graph ‘x’ versus ‘y’. We give the random values for ‘x’ and we find the value of ‘f(x)’. We can give all real numbers for the value of ‘x’. Thus we will have coordinate points (x, y) (here ‘y’ is f(x)). Hence, we can plot the graph by using the values. We can also draw the graph using the intercept method.
Complete step by step answer:
Given \[f(x) = - 4x\]. Let's give the values for ‘x’ and we find the value of ‘f(x)’.
Put \[x = 1\] in \[f(x) = - 4x\] we have,
\[f(1) = - 4 \times (1) = - 4\]
Thus we have coordinate points \[(1, - 4)\].
Put \[x = - 1\]in \[f(x) = - 4x\] we have,
\[f( - 1) = - 4 \times ( - 1) = 4\]
Thus we have coordinate points \[( - 1,4)\].
Put \[x = 2\] in \[f(x) = - 4x\] we have,
\[f(2) = - 4 \times (2) = - 8\]
Thus we have coordinate points \[(2, - 8)\].
Put \[x = - 2\]in \[f(x) = - 4x\] we have,
\[f( - 2) = - 4 \times ( - 2) = 8\]
Thus we have coordinate points \[( - 2,8)\].
Put \[x = 3\] in \[f(x) = - 4x\] we have,
\[f(3) = - 4 \times (3) = - 12\]
Thus we have a coordinate point after rounding off is \[(3, - 12)\].
Put \[x = - 3\]in \[f(x) = - 4x\] we have,
\[f( - 3) = - 4 \times ( - 3) = 12\]
Thus we have coordinate point after rounding off is \[( - 3,12)\].Thus we have,
Let’s draw the graph for these coordinates,
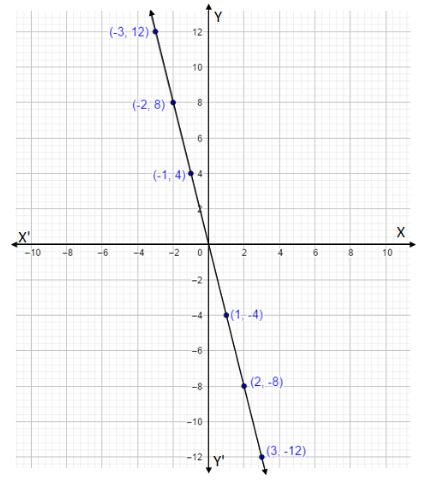
Note:A graph shows the relation between two variable quantities, it contains two axes perpendicular to each other namely the x-axis and the y-axis. Each variable is measured along one of the axes. In the question, we are given one linear equation containing two variables namely x and y, x is measured along the x-axis and y is measured along the y-axis while tracing the given equations.
Complete step by step answer:
Given \[f(x) = - 4x\]. Let's give the values for ‘x’ and we find the value of ‘f(x)’.
Put \[x = 1\] in \[f(x) = - 4x\] we have,
\[f(1) = - 4 \times (1) = - 4\]
Thus we have coordinate points \[(1, - 4)\].
Put \[x = - 1\]in \[f(x) = - 4x\] we have,
\[f( - 1) = - 4 \times ( - 1) = 4\]
Thus we have coordinate points \[( - 1,4)\].
Put \[x = 2\] in \[f(x) = - 4x\] we have,
\[f(2) = - 4 \times (2) = - 8\]
Thus we have coordinate points \[(2, - 8)\].
Put \[x = - 2\]in \[f(x) = - 4x\] we have,
\[f( - 2) = - 4 \times ( - 2) = 8\]
Thus we have coordinate points \[( - 2,8)\].
Put \[x = 3\] in \[f(x) = - 4x\] we have,
\[f(3) = - 4 \times (3) = - 12\]
Thus we have a coordinate point after rounding off is \[(3, - 12)\].
Put \[x = - 3\]in \[f(x) = - 4x\] we have,
\[f( - 3) = - 4 \times ( - 3) = 12\]
Thus we have coordinate point after rounding off is \[( - 3,12)\].Thus we have,
| \[x\] | \[1\] | \[ - 1\] | \[2\] | \[ - 2\] | \[3\] | \[ - 3\] |
| \[y = f(x)\] | \[ - 4\] | \[4\] | \[ - 8\] | \[8\] | \[ - 12\] | \[12\] |
Let’s draw the graph for these coordinates,

Note:A graph shows the relation between two variable quantities, it contains two axes perpendicular to each other namely the x-axis and the y-axis. Each variable is measured along one of the axes. In the question, we are given one linear equation containing two variables namely x and y, x is measured along the x-axis and y is measured along the y-axis while tracing the given equations.
Recently Updated Pages
Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Master Class 9 English: Engaging Questions & Answers for Success

Master Class 9 Maths: Engaging Questions & Answers for Success

Master Class 9 Social Science: Engaging Questions & Answers for Success

List of National & International Important Days

Master Class 10 Computer Science: Engaging Questions & Answers for Success

Trending doubts
Difference Between Plant Cell and Animal Cell

Fill the blanks with the suitable prepositions 1 The class 9 english CBSE

Name 10 Living and Non living things class 9 biology CBSE

The highest mountain peak in India is A Kanchenjunga class 9 social science CBSE

On an outline map of India show its neighbouring c class 9 social science CBSE

Write the 6 fundamental rights of India and explain in detail




