
How do you graph the equation $y=5x-3$?
Answer
532.5k+ views
Change of form of the given equation will give the x-intercept and y-intercept of the line $y=5x-3$. We change it to the form of $\dfrac{x}{p}+\dfrac{y}{q}=1$ to find the x-intercept, and y-intercept of the line as $p$ and $q$ respectively. then we place the points on the axes and from there we draw the line on the graph.
Complete step by step answer:
We are taking the general equation of a line to understand the slope and the intercept form of the line $y=5x-3$. The given equation is in the form of $y=mx+k$. m is the slope of the line. The slope of the line is $5$.
We have to find the x-intercept and y-intercept of the line $y=5x-3$.
For this we convert the given equation into the form of $\dfrac{x}{p}+\dfrac{y}{q}=1$. From the form we get that the x intercept, and y intercept of the line will be$p$ and $q$ respectively. The points will be $\left( p,0 \right),\left( 0,q \right)$.
The given equation is $y=5x-3$. Converting into the form of $\dfrac{x}{p}+\dfrac{y}{q}=1$, we get
$\begin{align}
& y=5x-3 \\
& \Rightarrow 5x-y=3 \\
& \Rightarrow \dfrac{x}{{}^{3}/{}_{5}}+\dfrac{y}{-3}=1 \\
\end{align}$
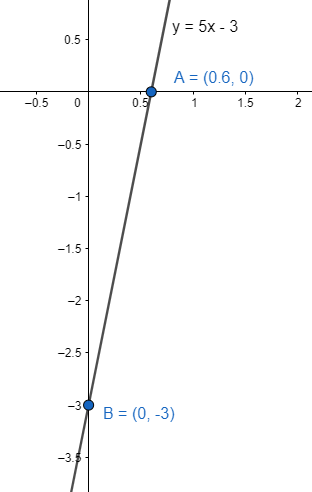
Therefore, the x intercept, and y intercept of the line $y=5x-3$ is $\dfrac{3}{5}$ and 3 respectively. The axes intersecting points are $\left( \dfrac{3}{5},0 \right),\left( 0,-3 \right)$.
Note:
A line parallel to the X-axis does not intersect the X-axis at any finite distance. Hence, we cannot get any finite x-intercept of such a line. The same goes for lines parallel to the Y-axis. In the case of the slope of a line, the range of the slope is 0 to $\infty $.
Complete step by step answer:
We are taking the general equation of a line to understand the slope and the intercept form of the line $y=5x-3$. The given equation is in the form of $y=mx+k$. m is the slope of the line. The slope of the line is $5$.
We have to find the x-intercept and y-intercept of the line $y=5x-3$.
For this we convert the given equation into the form of $\dfrac{x}{p}+\dfrac{y}{q}=1$. From the form we get that the x intercept, and y intercept of the line will be$p$ and $q$ respectively. The points will be $\left( p,0 \right),\left( 0,q \right)$.
The given equation is $y=5x-3$. Converting into the form of $\dfrac{x}{p}+\dfrac{y}{q}=1$, we get
$\begin{align}
& y=5x-3 \\
& \Rightarrow 5x-y=3 \\
& \Rightarrow \dfrac{x}{{}^{3}/{}_{5}}+\dfrac{y}{-3}=1 \\
\end{align}$
Therefore, the x intercept, and y intercept of the line $y=5x-3$ is $\dfrac{3}{5}$ and 3 respectively. The axes intersecting points are $\left( \dfrac{3}{5},0 \right),\left( 0,-3 \right)$.

Note:
A line parallel to the X-axis does not intersect the X-axis at any finite distance. Hence, we cannot get any finite x-intercept of such a line. The same goes for lines parallel to the Y-axis. In the case of the slope of a line, the range of the slope is 0 to $\infty $.
Recently Updated Pages
The height of a solid metal cylinder is 20cm Its r-class-10-maths-ICSE

If a train crossed a pole at a speed of 60kmhr in 30 class 10 physics CBSE

Name the Writs that the High Courts are empowered to class 10 social science CBSE

A tower is 5sqrt 3 meter high Find the angle of el-class-10-maths-CBSE

Immediate cause of variations of A Mutations B Environmental class 10 biology CBSE

A rectangular container whose base is a square of side class 10 maths CBSE

Trending doubts
Why is there a time difference of about 5 hours between class 10 social science CBSE

Why is Sardar Vallabhbhai Patel called the Iron man class 10 social science CBSE

Tropical deciduous trees shed their leaves in the dry class 10 social science CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

Write a letter to the principal requesting him to grant class 10 english CBSE

Leap year has days A 365 B 366 C 367 D 368 class 10 maths CBSE




