
Greenville is 1,200 miles west and 90 miles north of Johnson City. How long is a direct straight-line route from Greenville to Johnson City?
Answer
507.9k+ views
Hint: The right approach to the above numerical is to sketch the route map. The problem is solved according to the geometrical figure we get upon the sketch. In this problem, we get a right-angle triangle. The third side of a right-angled triangle can be found out by the Pythagoras theorem.
Complete step by step solution:
Using the cardinal directions listed below,
We draw the diagram.
According to our question,
Greenville is 1200 miles west and is 90 miles from Johnson City. we are asked to find the distance between Greenville and Johnson.
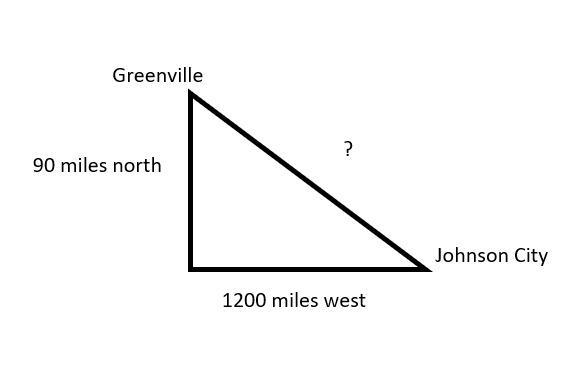
The diagram has one right angle and is a right-angled triangle.
Given that the 2 sides of the triangle are known.
The length of the first side of the triangle is 1200 miles.
The length of the second side of the triangle is 90 miles.
We need to find out the length of the third side of the triangle.
The length of the third side of a right-angled triangle can be found out by Pythagoras Theorem.
Pythagoras Theorem:
This Theorem defines the relationship between the three sides of a triangle.
It states that the square of the hypotenuse of the right-angled triangle is equal to the sum of the squares of the other two sides of a triangle.
The other two sides of a triangle are designated as base and height of a triangle, respectively.
According to Pythagoras Theorem,
${{\left( hypotenuse \right)}^{2}}={{\left( base \right)}^{2}}+{{\left( height \right)}^{2}}$
In the given question,
base = 1200 miles
height = 90 miles
hypotenuse = x?
$\Rightarrow {{\left( x \right)}^{2}}={{\left( 1200 \right)}^{2}}+{{\left( 90 \right)}^{2}}$
Now start evaluating,
$\Rightarrow {{\left( x \right)}^{2}}=1440000+8100$
$\Rightarrow {{\left( x \right)}^{2}}=1448100$
Now apply root on both sides of the equation.
$\Rightarrow x=\sqrt{1448100}$
hypotenuse = 1203.37 miles.
Thus, the length of the direct straight-line route from Greenville to Johnson City is 1203.37 miles.
Note: We must mark the directions and routes very precisely while making a sketch or drawing a diagram. For any right-angled triangle, the hypotenuse is the length of the longest side of the triangle. Pythagoras theorem is valid only in the case of the right-angled triangle.
Complete step by step solution:
Using the cardinal directions listed below,
We draw the diagram.

According to our question,
Greenville is 1200 miles west and is 90 miles from Johnson City. we are asked to find the distance between Greenville and Johnson.

The diagram has one right angle and is a right-angled triangle.
Given that the 2 sides of the triangle are known.
The length of the first side of the triangle is 1200 miles.
The length of the second side of the triangle is 90 miles.
We need to find out the length of the third side of the triangle.
The length of the third side of a right-angled triangle can be found out by Pythagoras Theorem.
Pythagoras Theorem:
This Theorem defines the relationship between the three sides of a triangle.
It states that the square of the hypotenuse of the right-angled triangle is equal to the sum of the squares of the other two sides of a triangle.
The other two sides of a triangle are designated as base and height of a triangle, respectively.
According to Pythagoras Theorem,
${{\left( hypotenuse \right)}^{2}}={{\left( base \right)}^{2}}+{{\left( height \right)}^{2}}$
In the given question,
base = 1200 miles
height = 90 miles
hypotenuse = x?
$\Rightarrow {{\left( x \right)}^{2}}={{\left( 1200 \right)}^{2}}+{{\left( 90 \right)}^{2}}$
Now start evaluating,
$\Rightarrow {{\left( x \right)}^{2}}=1440000+8100$
$\Rightarrow {{\left( x \right)}^{2}}=1448100$
Now apply root on both sides of the equation.
$\Rightarrow x=\sqrt{1448100}$
hypotenuse = 1203.37 miles.
Thus, the length of the direct straight-line route from Greenville to Johnson City is 1203.37 miles.
Note: We must mark the directions and routes very precisely while making a sketch or drawing a diagram. For any right-angled triangle, the hypotenuse is the length of the longest side of the triangle. Pythagoras theorem is valid only in the case of the right-angled triangle.
Recently Updated Pages
How do you convert r6sec theta into Cartesian form class 10 maths CBSE

How do you solve dfrac5y3dfracy+72y6+1 and find any class 10 maths CBSE

If sin A+B1 and cos AB1 0circ le left A+B rightle 90circ class 10 maths CBSE

On the number line 10 is to the of zero class 10 maths CBSE

How do you solve 5xge 30 class 10 maths CBSE

In the following sentence supply a verb in agreement class 10 english CBSE

Trending doubts
Write an application to the principal requesting five class 10 english CBSE

Why is there a time difference of about 5 hours between class 10 social science CBSE

Write a letter to the principal requesting him to grant class 10 english CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

What is the median of the first 10 natural numbers class 10 maths CBSE

Write examples of herbivores carnivores and omnivo class 10 biology CBSE




