
How do you graph and solve $y = \left| { - \dfrac{1}{4}x - 1} \right|$?
Answer
526.8k+ views
Hint: Plotting a graph depends on the type of equation we have. In the problem, we have a linear equation of the absolute function. Here, first, we have to explain the modulus function which is . Now for different values of $x$ find $y = f\left( x \right)$. After that use the points to plot the graph.
Complete step-by-step solution:
Now, we can define the modulus function.
The modulus function generally refers to the function that gives the positive value of any variable or a number. Also known as the absolute value function, it can generate a non-negative value for any independent variable, irrespective of it being positive or negative. Commonly represented as: \[y = \left| x \right|\], where x represents a real number, and \[y = f\left( x \right)\], representing all positive real numbers.
The expression in which a modulus can be defined is:
First take -1 common from the right side,
$ \Rightarrow y = \left| { - 1\left( {\dfrac{1}{4}x + 1} \right)} \right|$
Break the terms,
$ \Rightarrow y = \left| { - 1} \right|\left| {\dfrac{1}{4}x + 1} \right|$
As we know, $\left| { - 1} \right| = 1$. Then,
$ \Rightarrow y = \left| {\dfrac{1}{4}x + 1} \right|$
Now, let us check $y$ for different values of $x$.
Consider, $x = - 4$, we have $x < 0,y = \left| {\dfrac{1}{4}x + 1} \right|$
$ \Rightarrow y = - \left( { - \dfrac{1}{4} \times 4 + 1} \right)$
Simplify the terms,
$ \Rightarrow y = - \left( { - 1 + 1} \right)$
Subtract the terms,
$ \Rightarrow y = 0$
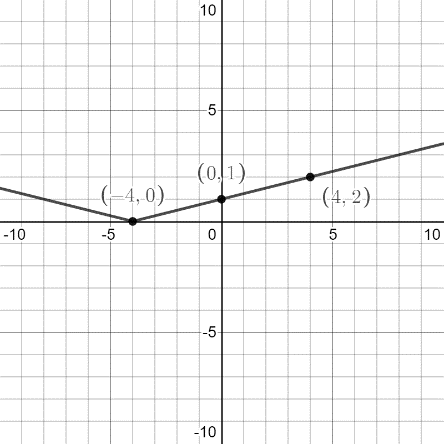
So, the point is (-4, 0).
Consider, $x = 0$, we have $x \ge 0,y = \left| {\dfrac{1}{4}x + 1} \right|$
$ \Rightarrow y = \left( {\dfrac{1}{4} \times 0 + 1} \right)$
Simplify the terms,
$ \Rightarrow y = 1$
So, the point is (0, 1).
Consider, $x = 4$, we have $x \ge 0,y = \left| {\dfrac{1}{4}x + 1} \right|$
$ \Rightarrow y = \left( {\dfrac{1}{4} \times 4 + 1} \right)$
Simplify the terms,
$ \Rightarrow y = \left( {1 + 1} \right)$
Add the terms,
$ \Rightarrow y = 2$
So, the point is (4, 2).
So, we draw the table for x and y.
We plot the above points and join them to have the graph as
Note: To solve a quadratic equation student can use the factorization method, completing the square method or quadratic formula method. When the time is less and we are sure about the quadratic formula, then it is best to use this method. We can cross verify the factors by opening parenthesis and solving.
Complete step-by-step solution:
Now, we can define the modulus function.
The modulus function generally refers to the function that gives the positive value of any variable or a number. Also known as the absolute value function, it can generate a non-negative value for any independent variable, irrespective of it being positive or negative. Commonly represented as: \[y = \left| x \right|\], where x represents a real number, and \[y = f\left( x \right)\], representing all positive real numbers.
The expression in which a modulus can be defined is:
First take -1 common from the right side,
$ \Rightarrow y = \left| { - 1\left( {\dfrac{1}{4}x + 1} \right)} \right|$
Break the terms,
$ \Rightarrow y = \left| { - 1} \right|\left| {\dfrac{1}{4}x + 1} \right|$
As we know, $\left| { - 1} \right| = 1$. Then,
$ \Rightarrow y = \left| {\dfrac{1}{4}x + 1} \right|$
Now, let us check $y$ for different values of $x$.
Consider, $x = - 4$, we have $x < 0,y = \left| {\dfrac{1}{4}x + 1} \right|$
$ \Rightarrow y = - \left( { - \dfrac{1}{4} \times 4 + 1} \right)$
Simplify the terms,
$ \Rightarrow y = - \left( { - 1 + 1} \right)$
Subtract the terms,
$ \Rightarrow y = 0$
So, the point is (-4, 0).
Consider, $x = 0$, we have $x \ge 0,y = \left| {\dfrac{1}{4}x + 1} \right|$
$ \Rightarrow y = \left( {\dfrac{1}{4} \times 0 + 1} \right)$
Simplify the terms,
$ \Rightarrow y = 1$
So, the point is (0, 1).
Consider, $x = 4$, we have $x \ge 0,y = \left| {\dfrac{1}{4}x + 1} \right|$
$ \Rightarrow y = \left( {\dfrac{1}{4} \times 4 + 1} \right)$
Simplify the terms,
$ \Rightarrow y = \left( {1 + 1} \right)$
Add the terms,
$ \Rightarrow y = 2$
So, the point is (4, 2).
So, we draw the table for x and y.
| X | -4 | 0 | 4 |
| Y | 0 | 1 | 2 |
We plot the above points and join them to have the graph as

Note: To solve a quadratic equation student can use the factorization method, completing the square method or quadratic formula method. When the time is less and we are sure about the quadratic formula, then it is best to use this method. We can cross verify the factors by opening parenthesis and solving.
Recently Updated Pages
How do you convert r6sec theta into Cartesian form class 10 maths CBSE

How do you solve dfrac5y3dfracy+72y6+1 and find any class 10 maths CBSE

If sin A+B1 and cos AB1 0circ le left A+B rightle 90circ class 10 maths CBSE

On the number line 10 is to the of zero class 10 maths CBSE

How do you solve 5xge 30 class 10 maths CBSE

In the following sentence supply a verb in agreement class 10 english CBSE

Trending doubts
Write an application to the principal requesting five class 10 english CBSE

Why is there a time difference of about 5 hours between class 10 social science CBSE

Write a letter to the principal requesting him to grant class 10 english CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

What is the median of the first 10 natural numbers class 10 maths CBSE

Write examples of herbivores carnivores and omnivo class 10 biology CBSE




