Question

Given here are some figures:

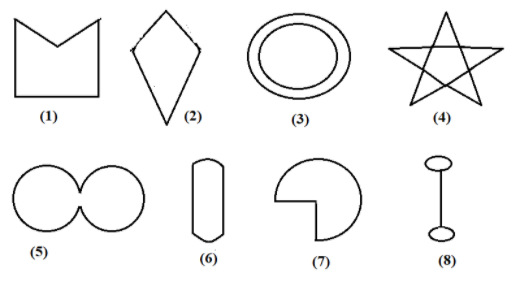
Classify each of them on the basis of the following:
i) Simple curve
ii) Simple closed curve
iii) Polygon
iv) Convex polygon
v) Concave polygon

Answer 1

Hint:
Recall from the definition that a simple curve is a curve that does not cross itself, a closed curve is the one that starts and end from the same point. A polygon is made up of line segments and vertices. Also, if each interior angle of the polygon is less than ${180^ \circ }$, then it is a convex polygon and if one of the angles of a polygon is greater than ${180^ \circ }$, then it is a concave polygon.

Complete step by step solution:
We know that a curve is a simple curve when it does not crosses itself.
Here, the figures (1), (2), (5), (6) and (7) are simple figures.
Also, a simple curve which starts and ends with the same point is a simple closed curve.
Here, the simple closed curves are figures (1), (2), (5), (6) and (7)
Next, a polygon is a two-dimensional closed figure which has straight lines as sides and has vertices.
The figures (1) and (2) are polygons.
A polygon in which every interior angle is less than ${180^ \circ }$ is a convex polygon.
There is only one figure that has each of its interior angle less than ${180^ \circ }$is the figure (2)
Now, find the polygon with at least one of the interior angles greater than ${180^ \circ }$, which is known as a concave polygon.
Here, figure(1) represents a concave polygon.

Note:
When we move to higher studies, the meaning of closed curves, simple curves and smooth curves modified a little bit. Just to solve such problems one must know the definitions and know how to apply the definition.