
Given, \[ABC\] is a triangle and \[PQ\] is a straight line meeting \[AB\] in \[P\] and \[AC\] in \[Q\] . If \[AP = 1{\text{ cm}}\], \[PB = 3{\text{ cm}}\], \[AQ = 1.5{\text{ cm}}\], \[QC = 4.5{\text{ cm}}\], prove that the area of \[\vartriangle APQ\] is one-sixteenth of the area of \[\vartriangle ABC\] .
Answer
469.2k+ views
Hint: Using a common angle and given values of different sides we will first prove the similarity in \[\vartriangle APQ\] and \[\vartriangle ABC\]. We will prove that the area of \[\vartriangle APQ\] is one-sixteenth of the area of \[\vartriangle ABC\] using similar triangle theorem which states that if two triangles are similar, then the ratio of the area of both triangles is proportional to the square of the ratio of their corresponding sides.
Complete answer:
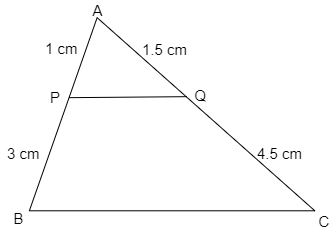
Given, \[AP = 1{\text{ cm}}\], \[PB = 3{\text{ cm}}\], \[AQ = 1.5{\text{ cm}}\] and \[QC = 4.5{\text{ cm}}\]
As \[AB = AP + PB\]
Putting the values of \[AP\] and \[PB\], we get
\[ \Rightarrow AB = 1 + 3\]
On adding we get
\[ \Rightarrow AB = 4{\text{ cm}}\]
Therefore,
\[\; \Rightarrow \dfrac{{AP}}{{PB}} = \dfrac{1}{4} - - - (1)\]
Similarly,
As \[AC = AQ + QC\]
Putting the values of \[AQ\] and \[QC\], we get
\[ \Rightarrow AC = 1.5 + 4.5\]
On adding we get
\[ \Rightarrow AC = 6{\text{ cm}}\]
Therefore,
\[ \Rightarrow \dfrac{{AQ}}{{AC}} = \dfrac{{1.5}}{6}\]
On simplification, we get
\[ \Rightarrow \dfrac{{AQ}}{{AC}} = \dfrac{1}{4} - - - (2)\]
Now, in \[\vartriangle APQ\] and \[\vartriangle ABC\]
\[\angle PAQ = \angle BAC\] (Common)
\[\dfrac{{AQ}}{{AC}} = \dfrac{{AP}}{{AB}}\] (From \[(1)\] and \[(2)\])
Therefore, by SAS similarity, we have
\[\vartriangle APQ \sim \vartriangle ABC\]
Since, we know by similar triangle theorem that when two triangles are similar then the ratio of the area of both triangles is proportional to the square of the ratio of their corresponding sides. Using this we can write that the ratio of the area of triangles \[\vartriangle APQ\] and \[\vartriangle ABC\] is proportional to the square of the ratio of their corresponding sides \[AP\] and \[AB\].
Therefore, we can write
\[ \Rightarrow \dfrac{{area\left( {\vartriangle APQ} \right)}}{{area\left( {\vartriangle ABC} \right)}} = \dfrac{{{{\left( {AP} \right)}^2}}}{{{{\left( {AB} \right)}^2}}}\]
Putting the value of \[AP = 1{\text{ cm}}\] and \[AB = 4{\text{ cm}}\] in above ratio, we get
\[ \Rightarrow \dfrac{{area\left( {\vartriangle APQ} \right)}}{{area\left( {\vartriangle ABC} \right)}} = \dfrac{{{{\left( 1 \right)}^2}}}{{{{\left( 4 \right)}^2}}}\]
On simplifying right hand side of the above equation
\[ \Rightarrow \dfrac{{area\left( {\vartriangle APQ} \right)}}{{area\left( {\vartriangle ABC} \right)}} = \dfrac{1}{{16}}\]
On taking \[area\left( {\vartriangle ABC} \right)\] to right hand side of the above equation, we get
\[ \Rightarrow area\left( {\vartriangle APQ} \right) = \dfrac{1}{{16}} \times area\left( {\vartriangle ABC} \right)\]
Hence, proved that the area of \[\vartriangle APQ\] is one-sixteenth of the area of \[\vartriangle ABC\] .
Note:
We can equate the ratio of the area of triangles \[\vartriangle APQ\] and \[\vartriangle ABC\] to the square of the ratio of any of their corresponding sides i.e., \[\dfrac{{area\left( {\vartriangle APQ} \right)}}{{area\left( {\vartriangle ABC} \right)}} = \dfrac{{{{\left( {AP} \right)}^2}}}{{{{\left( {AB} \right)}^2}}} = \dfrac{{{{\left( {AQ} \right)}^2}}}{{{{\left( {AC} \right)}^2}}} = \dfrac{{{{\left( {PQ} \right)}^2}}}{{{{\left( {BC} \right)}^2}}}\] . But here we have taken the ratio \[\dfrac{{{{\left( {AP} \right)}^2}}}{{{{\left( {AB} \right)}^2}}}\] because on squaring \[AP\] and \[AB\] and then taking the ratio \[\dfrac{{{{\left( {AP} \right)}^2}}}{{{{\left( {AB} \right)}^2}}}\] is easy while squaring the sides \[AQ\] and \[AC\] and then taking the ratio \[\dfrac{{{{\left( {AQ} \right)}^2}}}{{{{\left( {AC} \right)}^2}}}\] might complicate the calculations.
Complete answer:

Given, \[AP = 1{\text{ cm}}\], \[PB = 3{\text{ cm}}\], \[AQ = 1.5{\text{ cm}}\] and \[QC = 4.5{\text{ cm}}\]
As \[AB = AP + PB\]
Putting the values of \[AP\] and \[PB\], we get
\[ \Rightarrow AB = 1 + 3\]
On adding we get
\[ \Rightarrow AB = 4{\text{ cm}}\]
Therefore,
\[\; \Rightarrow \dfrac{{AP}}{{PB}} = \dfrac{1}{4} - - - (1)\]
Similarly,
As \[AC = AQ + QC\]
Putting the values of \[AQ\] and \[QC\], we get
\[ \Rightarrow AC = 1.5 + 4.5\]
On adding we get
\[ \Rightarrow AC = 6{\text{ cm}}\]
Therefore,
\[ \Rightarrow \dfrac{{AQ}}{{AC}} = \dfrac{{1.5}}{6}\]
On simplification, we get
\[ \Rightarrow \dfrac{{AQ}}{{AC}} = \dfrac{1}{4} - - - (2)\]
Now, in \[\vartriangle APQ\] and \[\vartriangle ABC\]
\[\angle PAQ = \angle BAC\] (Common)
\[\dfrac{{AQ}}{{AC}} = \dfrac{{AP}}{{AB}}\] (From \[(1)\] and \[(2)\])
Therefore, by SAS similarity, we have
\[\vartriangle APQ \sim \vartriangle ABC\]
Since, we know by similar triangle theorem that when two triangles are similar then the ratio of the area of both triangles is proportional to the square of the ratio of their corresponding sides. Using this we can write that the ratio of the area of triangles \[\vartriangle APQ\] and \[\vartriangle ABC\] is proportional to the square of the ratio of their corresponding sides \[AP\] and \[AB\].
Therefore, we can write
\[ \Rightarrow \dfrac{{area\left( {\vartriangle APQ} \right)}}{{area\left( {\vartriangle ABC} \right)}} = \dfrac{{{{\left( {AP} \right)}^2}}}{{{{\left( {AB} \right)}^2}}}\]
Putting the value of \[AP = 1{\text{ cm}}\] and \[AB = 4{\text{ cm}}\] in above ratio, we get
\[ \Rightarrow \dfrac{{area\left( {\vartriangle APQ} \right)}}{{area\left( {\vartriangle ABC} \right)}} = \dfrac{{{{\left( 1 \right)}^2}}}{{{{\left( 4 \right)}^2}}}\]
On simplifying right hand side of the above equation
\[ \Rightarrow \dfrac{{area\left( {\vartriangle APQ} \right)}}{{area\left( {\vartriangle ABC} \right)}} = \dfrac{1}{{16}}\]
On taking \[area\left( {\vartriangle ABC} \right)\] to right hand side of the above equation, we get
\[ \Rightarrow area\left( {\vartriangle APQ} \right) = \dfrac{1}{{16}} \times area\left( {\vartriangle ABC} \right)\]
Hence, proved that the area of \[\vartriangle APQ\] is one-sixteenth of the area of \[\vartriangle ABC\] .
Note:
We can equate the ratio of the area of triangles \[\vartriangle APQ\] and \[\vartriangle ABC\] to the square of the ratio of any of their corresponding sides i.e., \[\dfrac{{area\left( {\vartriangle APQ} \right)}}{{area\left( {\vartriangle ABC} \right)}} = \dfrac{{{{\left( {AP} \right)}^2}}}{{{{\left( {AB} \right)}^2}}} = \dfrac{{{{\left( {AQ} \right)}^2}}}{{{{\left( {AC} \right)}^2}}} = \dfrac{{{{\left( {PQ} \right)}^2}}}{{{{\left( {BC} \right)}^2}}}\] . But here we have taken the ratio \[\dfrac{{{{\left( {AP} \right)}^2}}}{{{{\left( {AB} \right)}^2}}}\] because on squaring \[AP\] and \[AB\] and then taking the ratio \[\dfrac{{{{\left( {AP} \right)}^2}}}{{{{\left( {AB} \right)}^2}}}\] is easy while squaring the sides \[AQ\] and \[AC\] and then taking the ratio \[\dfrac{{{{\left( {AQ} \right)}^2}}}{{{{\left( {AC} \right)}^2}}}\] might complicate the calculations.
Recently Updated Pages
The height of a solid metal cylinder is 20cm Its r-class-10-maths-ICSE

If a train crossed a pole at a speed of 60kmhr in 30 class 10 physics CBSE

Name the Writs that the High Courts are empowered to class 10 social science CBSE

A tower is 5sqrt 3 meter high Find the angle of el-class-10-maths-CBSE

Immediate cause of variations of A Mutations B Environmental class 10 biology CBSE

A rectangular container whose base is a square of side class 10 maths CBSE

Trending doubts
Tropical deciduous trees shed their leaves in the dry class 10 social science CBSE

Which scientist proved that even plants have feelings class 10 physics CBSE

10 examples of evaporation in daily life with explanations

Write any two uses of Plaster of Paris class 10 chemistry CBSE

Five things I will do to build a great India class 10 english CBSE

In which situations is the process of fermentation class 10 biology CBSE




