
Find the volume \[({{m}^{3}})\] in a cube, one face of which has an area of \[64{{m}^{2}}\].
Answer
564.3k+ views
Hint: First of all, we should use the side of the cube as a. We should know the formulae of one face of the cube and the formulae for volume of cube. We should find the area of one face of the cube and volume of the cube in terms of a. We should equate the area of the cube obtained in terms of a to \[64{{m}^{2}}\]. By this, we have to find the value of a. With this value of a, we have to find the volume of the cube.
Complete step-by-step solution -
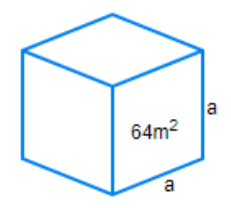
Before solving the question, we should know that the length, breadth and height of the cube are equal. We should also know the formula for area of base of cube and formula for volume of cube. We know that the base of the cube is a square. So, let us assume the side of a cube is equal to a. As the base of the cube is a square, the area of the base of the cube of side a is equal to the area of square of side a. So, the formula for the area of the base of the cube is equal to \[{{a}^{2}}\]. We know that the volume of a 3D figure is equal to the product of the area of base and its height. As the side of the cube is equal to a, the height of the cube is also equal to a. So, the volume of the cube is equal to \[{{a}^{3}}\].
So, it is clear that if side of cube = a
Area of one face of cube \[={{a}^{2}}\]
Volume of cube \[={{a}^{3}}\]
In the question, we are given that the area of one face of the cube is equal to \[64{{m}^{2}}\].
We know that the area of one face of a cube is equal to \[{{a}^{2}}\] if a is the side of the cube.
Hence, we get
\[\begin{align}
& {{a}^{2}}=64{{m}^{2}} \\
& \Rightarrow a=8m......(1) \\
\end{align}\]
We know that if a is the side of a cube, then the volume of the cube is equal to \[{{a}^{3}}\].
From equation (1), we get
\[\begin{align}
& \Rightarrow {{a}^{3}}={{(8m)}^{3}} \\
& \Rightarrow {{a}^{3}}=216{{m}^{3}} \\
\end{align}\]
Hence, the volume of the cube is equal to \[216{{m}^{3}}\].
Note: Students may go wrong by equating the area of the cube equal to \[64{{m}^{2}}\]. We know that the area of the cube is equal to \[6{{a}^{2}}\].
Now we will get
\[\begin{align}
& 6{{a}^{2}}=64 \\
& \Rightarrow {{a}^{2}}=\dfrac{64}{6} \\
& \Rightarrow a=\sqrt{\dfrac{64}{6}} \\
& \Rightarrow a=\dfrac{8}{\sqrt{6}} \\
\end{align}\]
From this we will get the value of a as \[\dfrac{8}{\sqrt{6}}\]. But the value of a is equal to 8 which is obtained in the above solution. So, we should be careful what is given in the question and we have to proceed accordingly.
Complete step-by-step solution -

Before solving the question, we should know that the length, breadth and height of the cube are equal. We should also know the formula for area of base of cube and formula for volume of cube. We know that the base of the cube is a square. So, let us assume the side of a cube is equal to a. As the base of the cube is a square, the area of the base of the cube of side a is equal to the area of square of side a. So, the formula for the area of the base of the cube is equal to \[{{a}^{2}}\]. We know that the volume of a 3D figure is equal to the product of the area of base and its height. As the side of the cube is equal to a, the height of the cube is also equal to a. So, the volume of the cube is equal to \[{{a}^{3}}\].
So, it is clear that if side of cube = a
Area of one face of cube \[={{a}^{2}}\]
Volume of cube \[={{a}^{3}}\]
In the question, we are given that the area of one face of the cube is equal to \[64{{m}^{2}}\].
We know that the area of one face of a cube is equal to \[{{a}^{2}}\] if a is the side of the cube.
Hence, we get
\[\begin{align}
& {{a}^{2}}=64{{m}^{2}} \\
& \Rightarrow a=8m......(1) \\
\end{align}\]
We know that if a is the side of a cube, then the volume of the cube is equal to \[{{a}^{3}}\].
From equation (1), we get
\[\begin{align}
& \Rightarrow {{a}^{3}}={{(8m)}^{3}} \\
& \Rightarrow {{a}^{3}}=216{{m}^{3}} \\
\end{align}\]
Hence, the volume of the cube is equal to \[216{{m}^{3}}\].
Note: Students may go wrong by equating the area of the cube equal to \[64{{m}^{2}}\]. We know that the area of the cube is equal to \[6{{a}^{2}}\].
Now we will get
\[\begin{align}
& 6{{a}^{2}}=64 \\
& \Rightarrow {{a}^{2}}=\dfrac{64}{6} \\
& \Rightarrow a=\sqrt{\dfrac{64}{6}} \\
& \Rightarrow a=\dfrac{8}{\sqrt{6}} \\
\end{align}\]
From this we will get the value of a as \[\dfrac{8}{\sqrt{6}}\]. But the value of a is equal to 8 which is obtained in the above solution. So, we should be careful what is given in the question and we have to proceed accordingly.
Recently Updated Pages
How do accretion disks form class 10 physics CBSE

How do you solve 7h + 2h 3 15 class 10 maths CBSE

How do you solve the following system of equations class 10 maths CBSE

Which is greater 03 or 04 class 10 maths CBSE

Choose the alternative which can replace the word printed class 10 english CBSE

Find the synonym of the underlined word Views regarding class 10 english CBSE

Trending doubts
Write an application to the principal requesting five class 10 english CBSE

Why is there a time difference of about 5 hours between class 10 social science CBSE

Write a letter to the principal requesting him to grant class 10 english CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

What is the median of the first 10 natural numbers class 10 maths CBSE

Write examples of herbivores carnivores and omnivo class 10 biology CBSE




