
Find the total surface area of a cone whose slant height is 9m and radius of the base is 14m.
Answer
512.4k+ views
Hint: The formula for the total surface area can be found out as $ A = \pi r\left( {r + l} \right) $ , where $ r $ is the radius of the base of the cone, $ l $ is slant height of the cone.
Complete step-by-step answer:
The slant height of the given cone is 9 m. Also, the radius of the base of the cone is given as 14 m.
As shown in the diagram, $ h $ is the slant height of the cone and $ r $ is the radius of the base of the cone.
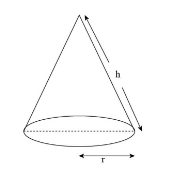
We know that the total surface area of the cone is given by $ A = \pi r\left( {r + l} \right) $
Now, we can substitute 9 for $ h $ and 14 for $ r $ , in the formula to find the total surface area of the cone.
Total surface area of the cone,
$
\Rightarrow A = \pi r\left( {r + l} \right)\\
= \pi \cdot 14\left( {14 + 9} \right)\\
= 14\pi \left( {23} \right)\\
= \dfrac{{22}}{7} \cdot 14 \cdot 23
$
Therefore, the total surface area of the cone is $ 1012{\rm{ }}{{\rm{m}}^2} $.
Additional Information:
A three-dimensional solid that tapers smoothly from a smooth circular base is called a cone.
The base shape of the cone is a circle. Cone has a single face and has a base similar to the cylinder.
The volume of a cone can be given by $ V = \dfrac{1}{3}\pi {r^2}h $ , where $ r $ is the radius of the base of the cone and $ h $ is the slant height of the cone. The total surface area of the cone is given by $ A = \pi r\left( {r + l} \right) $ .
Note: Remembering formulae becomes tedious sometimes and students often make mistakes while writing the formula for total surface area of the cone. If they understand how the formula has arrived, it would be easier for them to remember it.
There is a chance of calculation mistakes in this type of question, so handle the calculation part with care.
Complete step-by-step answer:
The slant height of the given cone is 9 m. Also, the radius of the base of the cone is given as 14 m.
As shown in the diagram, $ h $ is the slant height of the cone and $ r $ is the radius of the base of the cone.

We know that the total surface area of the cone is given by $ A = \pi r\left( {r + l} \right) $
Now, we can substitute 9 for $ h $ and 14 for $ r $ , in the formula to find the total surface area of the cone.
Total surface area of the cone,
$
\Rightarrow A = \pi r\left( {r + l} \right)\\
= \pi \cdot 14\left( {14 + 9} \right)\\
= 14\pi \left( {23} \right)\\
= \dfrac{{22}}{7} \cdot 14 \cdot 23
$
Therefore, the total surface area of the cone is $ 1012{\rm{ }}{{\rm{m}}^2} $.
Additional Information:
A three-dimensional solid that tapers smoothly from a smooth circular base is called a cone.
The base shape of the cone is a circle. Cone has a single face and has a base similar to the cylinder.
The volume of a cone can be given by $ V = \dfrac{1}{3}\pi {r^2}h $ , where $ r $ is the radius of the base of the cone and $ h $ is the slant height of the cone. The total surface area of the cone is given by $ A = \pi r\left( {r + l} \right) $ .
Note: Remembering formulae becomes tedious sometimes and students often make mistakes while writing the formula for total surface area of the cone. If they understand how the formula has arrived, it would be easier for them to remember it.
There is a chance of calculation mistakes in this type of question, so handle the calculation part with care.
Recently Updated Pages
Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Social Science: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Master Class 11 Physics: Engaging Questions & Answers for Success

Trending doubts
Difference Between Plant Cell and Animal Cell

Name 10 Living and Non living things class 9 biology CBSE

Fill the blanks with the suitable prepositions 1 The class 9 english CBSE

On an outline map of India show its neighbouring c class 9 social science CBSE

The highest mountain peak in India is A Kanchenjunga class 9 social science CBSE

Write the 6 fundamental rights of India and explain in detail




