
How do you find the other sides of a right triangle if the hypotenuse = 5 and the other sides = x, and the other two sides are also equilateral?
Answer
478.8k+ views
Hint: Here we have to find the other side of a right triangle. We have the value of hypotenuse and the other side of the triangle is equilateral. The equilateral means that they are equal. Hence by using the Pythagoras theorem we can determine the value of the other side.
Complete step by step solution:
In mathematics, the Pythagorean theorem, or Pythagoras's theorem, is a fundamental relation in Euclidean geometry among the three sides of a right triangle. It states that the area of the square whose side is the hypotenuse is equal to the sum of the areas of the squares on the other two sides. Therefore, we have \[A{B^2} = A{C^2} + B{C^2}\].
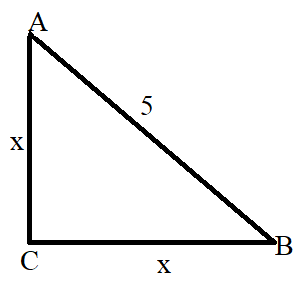
According to data of the question the value of \[AB = 5\]and the other sides of the triangle is equilateral, that is they are equal. therefore the value of \[AC = BC = x\].
By applying the Pythagoras theorem we have
\[A{B^2} = A{C^2} + B{C^2}\]
Substituting the values to the above inequality we have
\[ \Rightarrow {5^2} = {x^2} + {x^2}\]
Applying the square to LHS and adding the terms in RHS we get
\[\Rightarrow 25 = 2{x^2}\]
Divide the above equation by 2 we get
\[\Rightarrow 12.5 = {x^2}\]
Take square root to the above equation
\[\Rightarrow \sqrt {12.5} = x\]
Therefore the value of x is \[x = 3.5\], when we apply the square root and round off the number
So the value of x is \[\sqrt {12.5} \] or \[3.5\]
Hence we have determined the value of x of a right triangle.
Hence the value of x is \[\sqrt {12.5} \] or \[3.5\]
Note: In the triangle we have 3 different kinds of triangles based on the length of the triangle namely, Equilateral, isosceles and scalene. Where equilateral triangle means all the sides are equal. Isosceles triangle means only two sides are equal. Scalene triangle means all the sides are different.
Complete step by step solution:
In mathematics, the Pythagorean theorem, or Pythagoras's theorem, is a fundamental relation in Euclidean geometry among the three sides of a right triangle. It states that the area of the square whose side is the hypotenuse is equal to the sum of the areas of the squares on the other two sides. Therefore, we have \[A{B^2} = A{C^2} + B{C^2}\].
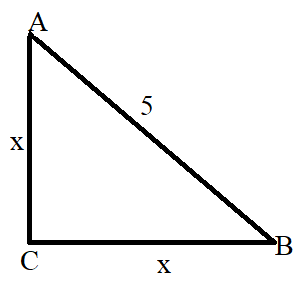
According to data of the question the value of \[AB = 5\]and the other sides of the triangle is equilateral, that is they are equal. therefore the value of \[AC = BC = x\].
By applying the Pythagoras theorem we have
\[A{B^2} = A{C^2} + B{C^2}\]
Substituting the values to the above inequality we have
\[ \Rightarrow {5^2} = {x^2} + {x^2}\]
Applying the square to LHS and adding the terms in RHS we get
\[\Rightarrow 25 = 2{x^2}\]
Divide the above equation by 2 we get
\[\Rightarrow 12.5 = {x^2}\]
Take square root to the above equation
\[\Rightarrow \sqrt {12.5} = x\]
Therefore the value of x is \[x = 3.5\], when we apply the square root and round off the number
So the value of x is \[\sqrt {12.5} \] or \[3.5\]
Hence we have determined the value of x of a right triangle.
Hence the value of x is \[\sqrt {12.5} \] or \[3.5\]
Note: In the triangle we have 3 different kinds of triangles based on the length of the triangle namely, Equilateral, isosceles and scalene. Where equilateral triangle means all the sides are equal. Isosceles triangle means only two sides are equal. Scalene triangle means all the sides are different.
Recently Updated Pages
Master Class 10 English: Engaging Questions & Answers for Success

Master Class 10 Social Science: Engaging Questions & Answers for Success

Master Class 10 Maths: Engaging Questions & Answers for Success

Master Class 10 Science: Engaging Questions & Answers for Success

Class 10 Question and Answer - Your Ultimate Solutions Guide

Master Class 10 Computer Science: Engaging Questions & Answers for Success

Trending doubts
Why is there a time difference of about 5 hours between class 10 social science CBSE

What is the scientific name of apple class 10 biology CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

Fill the blanks with proper collective nouns 1 A of class 10 english CBSE

Write examples of herbivores carnivores and omnivo class 10 biology CBSE

Give 10 examples of Material nouns Abstract nouns Common class 10 english CBSE




