
Find the area of the unshaded region if the radius of the circles and the semicircle is 3cm.
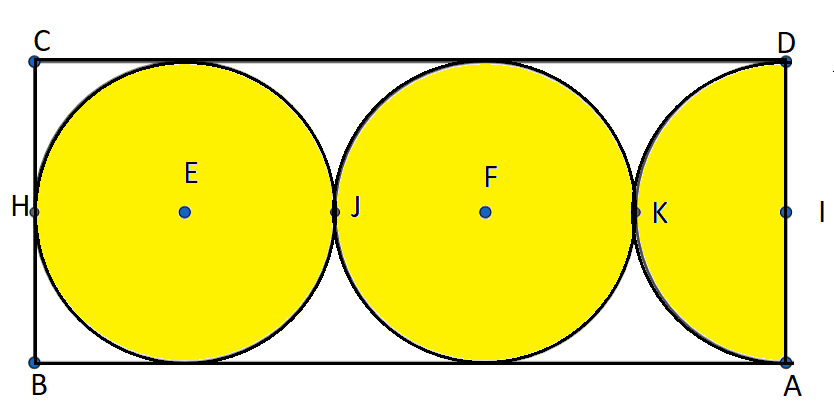

Answer
563.7k+ views
Hint: Observe that the area of the unshaded region is equal to the area of the shaded region subtracted from the area of the rectangle, i.e. .ar(Unshaded) = ar(ABCD) – ar(Shaded). Now observe that the shaded region consists of two circles and one semicircle. Use the fact that the area of a circle of radius r is equal to $\pi {{r}^{2}}$ to determine the area of the shaded region. Now observe that HIDC is also a rectangle and hence HI = CD. Hence find the length of CD. Again observe that LOBC is also a rectangle and hence BC = LO. Hence find the length of BC. Hence determine the area of the rectangle using the fact that the area of a rectangle of length l and breadth b is given by A = lb. Hence determine the area of the unshaded region.
Complete step by step solution:
We have a radius of circles = r = 3cm.
Now, we have the area of the shaded region = Area of two circles + Area of the semicircle.
We know that area of a circle of radius r $=\pi {{r}^{2}}$
Hence, we have
Area of the shaded region $=\pi {{r}^{2}}+\pi {{r}^{2}}+\dfrac{\pi {{r}^{2}}}{2}=2.5\pi {{r}^{2}}=2.5\times \pi \times {{3}^{2}}=22.5\pi $ square centimetres.
Also, we have HIDC as a rectangle.
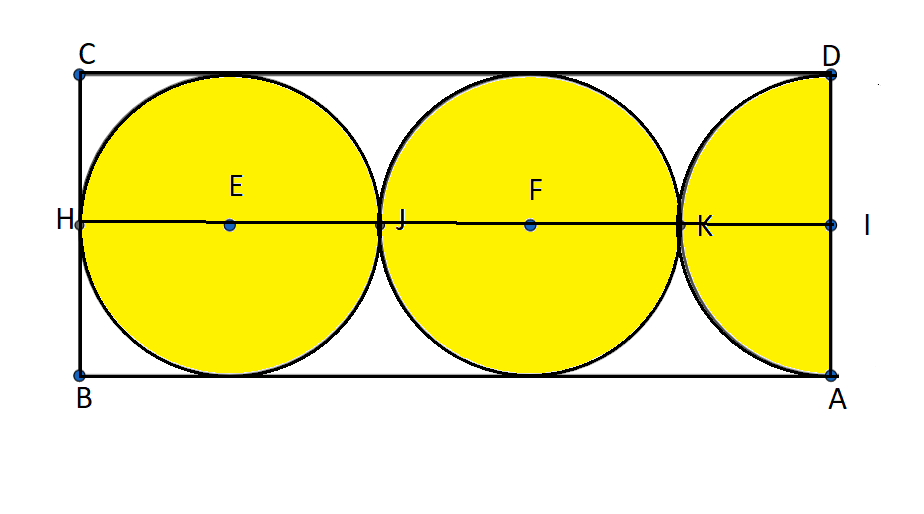
Hence, HI = DC(because the opposite side of a rectangle are equal)
Hence, we have DC = HE+EJ+JF+FK+KI = r+r+r+r+r = 5r = 15cm.
Hence, we have DC = 15cm
Also, we have LOBC as a rectangle and hence LO = BC.
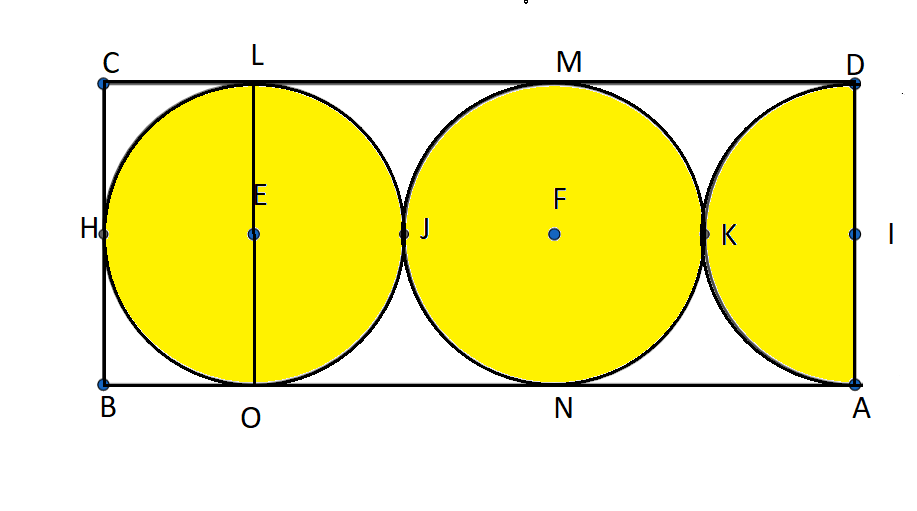
Hence, we have
BC = LE+EO = r+r = 2r.
We know that the area of a rectangle of length l and breadth b is given by A = lb
Hence, we have
The area of the rectangle $=5r\times 2r=10{{r}^{2}}=10\times 9=90$ square centimetres.
Now, we know that
ar(Unshaded) = ar(ABCD) – ar(Shaded)
Hence, we have
ar(Unshaded) $=90-22.5\pi $ square centimetres.
Note: In the questions of mensuration, we must take special care of the units of the parameters involved. Most students get incorrect results only because they do not take the units into consideration. In this question, although it is less likely to make a mistake in the units of the terms, a student can make a mistake in finding the length of the sides. One can hastily see that there are three circles(not noticing one is a semicircle ) and hence set the length of the side CD as 6r instead of the correct value 5r.
Complete step by step solution:
We have a radius of circles = r = 3cm.
Now, we have the area of the shaded region = Area of two circles + Area of the semicircle.
We know that area of a circle of radius r $=\pi {{r}^{2}}$
Hence, we have
Area of the shaded region $=\pi {{r}^{2}}+\pi {{r}^{2}}+\dfrac{\pi {{r}^{2}}}{2}=2.5\pi {{r}^{2}}=2.5\times \pi \times {{3}^{2}}=22.5\pi $ square centimetres.
Also, we have HIDC as a rectangle.

Hence, HI = DC(because the opposite side of a rectangle are equal)
Hence, we have DC = HE+EJ+JF+FK+KI = r+r+r+r+r = 5r = 15cm.
Hence, we have DC = 15cm
Also, we have LOBC as a rectangle and hence LO = BC.

Hence, we have
BC = LE+EO = r+r = 2r.
We know that the area of a rectangle of length l and breadth b is given by A = lb
Hence, we have
The area of the rectangle $=5r\times 2r=10{{r}^{2}}=10\times 9=90$ square centimetres.
Now, we know that
ar(Unshaded) = ar(ABCD) – ar(Shaded)
Hence, we have
ar(Unshaded) $=90-22.5\pi $ square centimetres.
Note: In the questions of mensuration, we must take special care of the units of the parameters involved. Most students get incorrect results only because they do not take the units into consideration. In this question, although it is less likely to make a mistake in the units of the terms, a student can make a mistake in finding the length of the sides. One can hastily see that there are three circles(not noticing one is a semicircle ) and hence set the length of the side CD as 6r instead of the correct value 5r.
Recently Updated Pages
How do you convert r6sec theta into Cartesian form class 10 maths CBSE

How do you solve dfrac5y3dfracy+72y6+1 and find any class 10 maths CBSE

If sin A+B1 and cos AB1 0circ le left A+B rightle 90circ class 10 maths CBSE

On the number line 10 is to the of zero class 10 maths CBSE

How do you solve 5xge 30 class 10 maths CBSE

In the following sentence supply a verb in agreement class 10 english CBSE

Trending doubts
Write an application to the principal requesting five class 10 english CBSE

Why is there a time difference of about 5 hours between class 10 social science CBSE

List of Lok Sabha Speakers of India

Which one of the following is the deepest seaport of class 10 social science CBSE

Write a letter to the principal requesting him to grant class 10 english CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths




