
What is the electric potential energy of the charge configuration as shown in the figure? Assume that
$q_1=+1.0\times 10^{-8}C$, $q_2=-2.0\times 10^{-8}C$, $q_3=+3.0\times 10^{-8}C$, $q_4=+2.0\times 10^{-8}C$and $a=1.0m$
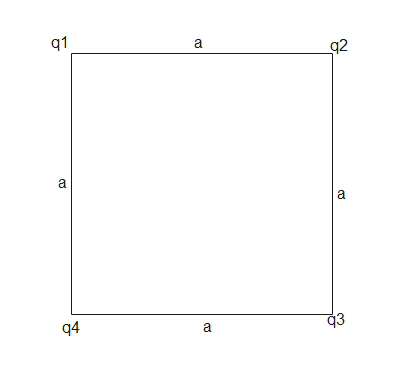

Answer
448.5k+ views
Hint: We know that the potential difference between two points in any electrical circuit is defined as the energy required to move a unit positive charge between the two points and potential energy is the energy stored by the system to do the same. Here, using the formula for the potential energy , we can find the net potential energy at the centre of the square as discussed below.
Formula used:
$P.E=\dfrac{kq_1q_2}{r}$
Complete step by step solution:
Given that, $q_1=+1.0\times 10^{-8}C$, $q_2=-2.0\times 10^{-8}C$, $q_3=+3.0\times 10^{-8}C$, $q_4=+2.0\times 10^{-8}C$and $a=1.0m$, then the centre of the square will be $O$ and the distance of the diagonals will be $\sqrt 2$, as shown in the figure below
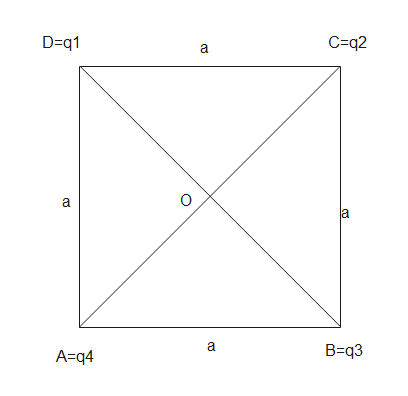
Then the potential difference at the O due to the charges will be the sum of potential energies at the centre which is given as
$T.P.E=P.E_{AB}+P.E_{BC}+P.E_{CD}+P.E_{DA}+P.E_{AC}+P.E_{DB}$
Substituting, for $P.E=\dfrac{kq_1q_2}{r}$ using the given we have
$\implies T.P.E=\dfrac{k\times 2\times 10^{-8}\times 3\times 10^{-8}}{1}+\dfrac{k\times -2\times 10^{-8}\times 3\times 10^{-8}}{1}+\dfrac{k\times -2\times 10^{-8}\times 1\times 10^{-8}}{1}+\dfrac{k\times 1\times 10^{-8}\times 2\times 10^{-8}}{1}+\dfrac{k\times 2\times 10^{-8}\times -2\times 10^{-8}}{\sqrt 2}+\dfrac{k\times 1\times 10^{-8}\times 3\times 10^{-8}}{\sqrt 2}$
$\implies T.P.E=\dfrac{k\times 6\times 10^{-16}}{1}+\dfrac{k\times -6\times 10^{-16}}{1}+\dfrac{k\times -2\times 10^{-16}}{1}+\dfrac{k\times 2\times 10^{-16}}{1}+\dfrac{k\times -4\times 10^{-16}}{\sqrt 2}+\dfrac{k\times 3\times 10^{-16}}{\sqrt 2}$on simplification, we get
$\implies T.P.E=\dfrac{k\times -4\times 10^{-16}}{\sqrt 2}+\dfrac{k\times 3\times 10^{-16}}{\sqrt 2}$
$\implies T.P.E=\dfrac{k\times 10^{-16}}{\sqrt 2}\times (3-4)$
On further simplification, we have
$\implies T.P.E=\dfrac{k\times -1\times 10^{-16}}{\sqrt 2}$
Since $k=9\times 10^9$, substituting, we have
$\implies T.P.E=\dfrac{9\times 10^{9}\times -1\times 10^{-16}}{\sqrt 2} =\dfrac{9\times 10^{-7}}{\sqrt 2}$
$\therefore T.P.E =\dfrac{9\times 10^{-7}}{\sqrt 2}J$
Thus the required total potential energy at the centre of the given square with side $a=1.0m$$\dfrac{9\times 10^{-7}}{\sqrt 2}J$
Additional Information:
We also know that electric current is produced due to motion of charges. The two are related by Ohm's law.
Note: If the unit positive charge is moved from a region of high potential to a region of low potential, then the energy is emitted during the process, or work is done by the system. Similarly, if the unit positive charge is moved from a region of low potential to high potential, then energy is absorbed, or work is done on the system.
Formula used:
$P.E=\dfrac{kq_1q_2}{r}$
Complete step by step solution:
Given that, $q_1=+1.0\times 10^{-8}C$, $q_2=-2.0\times 10^{-8}C$, $q_3=+3.0\times 10^{-8}C$, $q_4=+2.0\times 10^{-8}C$and $a=1.0m$, then the centre of the square will be $O$ and the distance of the diagonals will be $\sqrt 2$, as shown in the figure below

Then the potential difference at the O due to the charges will be the sum of potential energies at the centre which is given as
$T.P.E=P.E_{AB}+P.E_{BC}+P.E_{CD}+P.E_{DA}+P.E_{AC}+P.E_{DB}$
Substituting, for $P.E=\dfrac{kq_1q_2}{r}$ using the given we have
$\implies T.P.E=\dfrac{k\times 2\times 10^{-8}\times 3\times 10^{-8}}{1}+\dfrac{k\times -2\times 10^{-8}\times 3\times 10^{-8}}{1}+\dfrac{k\times -2\times 10^{-8}\times 1\times 10^{-8}}{1}+\dfrac{k\times 1\times 10^{-8}\times 2\times 10^{-8}}{1}+\dfrac{k\times 2\times 10^{-8}\times -2\times 10^{-8}}{\sqrt 2}+\dfrac{k\times 1\times 10^{-8}\times 3\times 10^{-8}}{\sqrt 2}$
$\implies T.P.E=\dfrac{k\times 6\times 10^{-16}}{1}+\dfrac{k\times -6\times 10^{-16}}{1}+\dfrac{k\times -2\times 10^{-16}}{1}+\dfrac{k\times 2\times 10^{-16}}{1}+\dfrac{k\times -4\times 10^{-16}}{\sqrt 2}+\dfrac{k\times 3\times 10^{-16}}{\sqrt 2}$on simplification, we get
$\implies T.P.E=\dfrac{k\times -4\times 10^{-16}}{\sqrt 2}+\dfrac{k\times 3\times 10^{-16}}{\sqrt 2}$
$\implies T.P.E=\dfrac{k\times 10^{-16}}{\sqrt 2}\times (3-4)$
On further simplification, we have
$\implies T.P.E=\dfrac{k\times -1\times 10^{-16}}{\sqrt 2}$
Since $k=9\times 10^9$, substituting, we have
$\implies T.P.E=\dfrac{9\times 10^{9}\times -1\times 10^{-16}}{\sqrt 2} =\dfrac{9\times 10^{-7}}{\sqrt 2}$
$\therefore T.P.E =\dfrac{9\times 10^{-7}}{\sqrt 2}J$
Thus the required total potential energy at the centre of the given square with side $a=1.0m$$\dfrac{9\times 10^{-7}}{\sqrt 2}J$
Additional Information:
We also know that electric current is produced due to motion of charges. The two are related by Ohm's law.
Note: If the unit positive charge is moved from a region of high potential to a region of low potential, then the energy is emitted during the process, or work is done by the system. Similarly, if the unit positive charge is moved from a region of low potential to high potential, then energy is absorbed, or work is done on the system.
Recently Updated Pages
Master Class 12 Biology: Engaging Questions & Answers for Success

Master Class 12 Physics: Engaging Questions & Answers for Success

Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Trending doubts
Which are the Top 10 Largest Countries of the World?

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE

Why is the cell called the structural and functional class 12 biology CBSE

Sketch the electric field lines in case of an electric class 12 physics CBSE

State and explain Coulombs law in electrostatics class 12 physics CBSE

a Tabulate the differences in the characteristics of class 12 chemistry CBSE




