
Draw phasor diagram for a series LCR circuit with alternating voltage source, determine the expression for the impedance of the circuit.
Answer
540k+ views
Hint: For getting the phasor diagram for the given conditions we will first apply the kvl across the circuit and then from the equations obtained from the kvl we will also get the expressions for the series impedance.
Complete step-by-step answer:
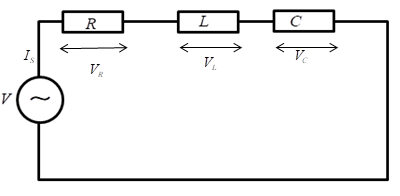
The voltage across each element in the circuit is given by
Let ${I_s} = {I_0}\sin \left( {\omega t} \right)$
Applying KVL in the above circuit
$V = {V_R} + {V_L} + {V_C}..................\left( 1 \right)$
Where
${V_R}$ is the voltage across the resistor
${V_L}$ is the voltage across inductor
${V_C}$ is the voltage across capacitor
Now according to Ohm’s law
V = IR
Now
The voltage across resistor
${V_R} = {I_s}R$
The voltage across inductor
${V_L} = {I_s}{X_L}$
${X_L}$ is the reactance of inductor
The voltage across capacitor
${V_c} = {I_s}{X_C}$
${X_C}$ is the reactance of the capacitor
Substituting these values in the equation (1)
$V = {I_s}R + {I_s}{X_L} + {I_s}{X_C}$
As we know the current leads the voltage by 90 degree in capacitor and lags by 90 degree in case of inductor.
So, taking the magnitude of above equation and assume ${X_L} > {X_C}$
$
V = \sqrt {{{\left( {{I_s}R} \right)}^2} + {{\left( {{I_s}{X_L} - {I_s}{X_C}} \right)}^2}} \\
V = {I_s}\sqrt {{R^2} + {{\left( {{X_L} - {X_C}} \right)}^2}} \\
\dfrac{V}{{{I_s}}} = \sqrt {{R^2} + {{\left( {{X_L} - {X_C}} \right)}^2}} \\
$
Let $\dfrac{V}{{{I_S}}} = Z$
$Z = \sqrt {{R^2} + {{\left( {{X_L} - {X_C}} \right)}^2}} $
Z is known as impedance.
The phasor diagram of the given circuit is shown below.
The resultant vector will be obtained by adding the two vectors ${V_L}$ and ${V_C}$
Because the two vectors are 180 degree apart as shown in the below figure
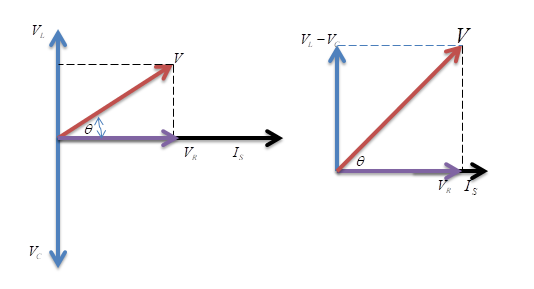
Note – While drawing the phasor diagram, the final reactive voltage must be positive in value therefore take the smallest voltage of the reactive element and subtract it from the largest voltage of the reactive element in the phasor diagram and then take the resultant using the Pythagoras theorem. The current vector is always in phase with the resistance voltage.
Complete step-by-step answer:

The voltage across each element in the circuit is given by
Let ${I_s} = {I_0}\sin \left( {\omega t} \right)$
Applying KVL in the above circuit
$V = {V_R} + {V_L} + {V_C}..................\left( 1 \right)$
Where
${V_R}$ is the voltage across the resistor
${V_L}$ is the voltage across inductor
${V_C}$ is the voltage across capacitor
Now according to Ohm’s law
V = IR
Now
The voltage across resistor
${V_R} = {I_s}R$
The voltage across inductor
${V_L} = {I_s}{X_L}$
${X_L}$ is the reactance of inductor
The voltage across capacitor
${V_c} = {I_s}{X_C}$
${X_C}$ is the reactance of the capacitor
Substituting these values in the equation (1)
$V = {I_s}R + {I_s}{X_L} + {I_s}{X_C}$
As we know the current leads the voltage by 90 degree in capacitor and lags by 90 degree in case of inductor.
So, taking the magnitude of above equation and assume ${X_L} > {X_C}$
$
V = \sqrt {{{\left( {{I_s}R} \right)}^2} + {{\left( {{I_s}{X_L} - {I_s}{X_C}} \right)}^2}} \\
V = {I_s}\sqrt {{R^2} + {{\left( {{X_L} - {X_C}} \right)}^2}} \\
\dfrac{V}{{{I_s}}} = \sqrt {{R^2} + {{\left( {{X_L} - {X_C}} \right)}^2}} \\
$
Let $\dfrac{V}{{{I_S}}} = Z$
$Z = \sqrt {{R^2} + {{\left( {{X_L} - {X_C}} \right)}^2}} $
Z is known as impedance.
The phasor diagram of the given circuit is shown below.
The resultant vector will be obtained by adding the two vectors ${V_L}$ and ${V_C}$
Because the two vectors are 180 degree apart as shown in the below figure

Note – While drawing the phasor diagram, the final reactive voltage must be positive in value therefore take the smallest voltage of the reactive element and subtract it from the largest voltage of the reactive element in the phasor diagram and then take the resultant using the Pythagoras theorem. The current vector is always in phase with the resistance voltage.
Recently Updated Pages
Master Class 12 Biology: Engaging Questions & Answers for Success

Master Class 12 Physics: Engaging Questions & Answers for Success

Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Trending doubts
Which are the Top 10 Largest Countries of the World?

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE

Why is the cell called the structural and functional class 12 biology CBSE

a Tabulate the differences in the characteristics of class 12 chemistry CBSE

Who discovered the cell and how class 12 biology CBSE

Draw a labelled sketch of the human eye class 12 physics CBSE




