
Draw a triangular prism and verify Euler’s Formula.
Answer
477k+ views
Hint:
We have to verify Euler’s Formula , for this we have to show that the number of faces, vertices, and edges of any polyhedron. It states that the sum of the number of faces and vertices is equal to the two more than the number of edges. Mathematically we can write , \[F{\text{ }} + {\text{ }}V{\text{ }} = {\text{ }}E{\text{ }} + {\text{ }}2,\] where $F$ is that the number of faces, \[V\] the number of vertices, and $E$ the number of edges.
Complete step by step solution:
Let us consider a triangular prism given below ,
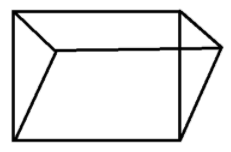
Now recall Euler’s formula, Either of two important mathematical theorems of Euler. the primary may be a topological invariance relating the number of faces, vertices, and edges of any polyhedron. It states that the sum of the number of faces and vertices is equal to the two more than the number of edges. Mathematically we can write , \[F{\text{ }} + {\text{ }}V{\text{ }} = {\text{ }}E{\text{ }} + {\text{ }}2,\] where $F$ is that the number of faces, \[V\] the number of vertices, and $E$ the number of edges. A cube, for instance, has six faces, eight vertices, and twelve edges, and satisfies this formula.
Therefore, consider \[F{\text{ }} + {\text{ }}V{\text{ }} = {\text{ }}E{\text{ }} + {\text{ }}2,\]
Here, In this triangular prism ,
The number of faces , $F = 5............(1)$
The number of vertices , $V = 6...............(2)$
Now, add $(1),(2)$ equations , we will get ,
$ \Rightarrow F + V = 5 + 6 = 11................(3)$
And the number of edges , $E = 9$
$ \Rightarrow E + 2 = 9 + 2 = 11...............(4)$
After comparing $(3)$ and $(4)$ , we can say that ,
Euler’s Formula is verified.
Note:
Questions similar in nature as that of above can be approached in a similar manner and we can solve it easily. For solving this type of question, we have to consider the polyhedron , so that we can count its edges, vertices and faces.
We have to verify Euler’s Formula , for this we have to show that the number of faces, vertices, and edges of any polyhedron. It states that the sum of the number of faces and vertices is equal to the two more than the number of edges. Mathematically we can write , \[F{\text{ }} + {\text{ }}V{\text{ }} = {\text{ }}E{\text{ }} + {\text{ }}2,\] where $F$ is that the number of faces, \[V\] the number of vertices, and $E$ the number of edges.
Complete step by step solution:
Let us consider a triangular prism given below ,

Now recall Euler’s formula, Either of two important mathematical theorems of Euler. the primary may be a topological invariance relating the number of faces, vertices, and edges of any polyhedron. It states that the sum of the number of faces and vertices is equal to the two more than the number of edges. Mathematically we can write , \[F{\text{ }} + {\text{ }}V{\text{ }} = {\text{ }}E{\text{ }} + {\text{ }}2,\] where $F$ is that the number of faces, \[V\] the number of vertices, and $E$ the number of edges. A cube, for instance, has six faces, eight vertices, and twelve edges, and satisfies this formula.
Therefore, consider \[F{\text{ }} + {\text{ }}V{\text{ }} = {\text{ }}E{\text{ }} + {\text{ }}2,\]
Here, In this triangular prism ,
The number of faces , $F = 5............(1)$
The number of vertices , $V = 6...............(2)$
Now, add $(1),(2)$ equations , we will get ,
$ \Rightarrow F + V = 5 + 6 = 11................(3)$
And the number of edges , $E = 9$
$ \Rightarrow E + 2 = 9 + 2 = 11...............(4)$
After comparing $(3)$ and $(4)$ , we can say that ,
Euler’s Formula is verified.
Note:
Questions similar in nature as that of above can be approached in a similar manner and we can solve it easily. For solving this type of question, we have to consider the polyhedron , so that we can count its edges, vertices and faces.
Recently Updated Pages
Master Class 10 English: Engaging Questions & Answers for Success

Master Class 10 Social Science: Engaging Questions & Answers for Success

Master Class 10 Maths: Engaging Questions & Answers for Success

Master Class 10 Science: Engaging Questions & Answers for Success

Class 10 Question and Answer - Your Ultimate Solutions Guide

Master Class 11 Economics: Engaging Questions & Answers for Success

Trending doubts
Why is there a time difference of about 5 hours between class 10 social science CBSE

What is the scientific name of apple class 10 biology CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

Fill the blanks with proper collective nouns 1 A of class 10 english CBSE

Write examples of herbivores carnivores and omnivo class 10 biology CBSE

Give 10 examples of Material nouns Abstract nouns Common class 10 english CBSE




