
Draw a pie chart for the following data:
Item of expenditure Food Health Clothing Education Savings Amount spent (in rupees) 3750 1875 1875 1200 7500
| Item of expenditure | Food | Health | Clothing | Education | Savings |
| Amount spent (in rupees) | 3750 | 1875 | 1875 | 1200 | 7500 |
Answer
421.5k+ views
Hint: Pie chart is drawn in a circle. So, first, we convert each item of expenditure into angle assuming the total angle in a circle \[{{360}^{0}}\] corresponds to income. Conversion of angle corresponding to the item is calculated by using the formula
\[\text{angle}=\dfrac{\text{amount spent on that item}}{\text{total income}}\times {{360}^{0}}\]
After finding the angle for each item of expenditure we divide the circle corresponds to that angle and gives a name to each part.
Complete step-by-step solution:
Let us assume\[I\] be the income.
Let us find the total income by adding the amount spent on each item as
\[\begin{align}
& \Rightarrow I=3,750+1,875+1,875+1,200+7,500 \\
& \Rightarrow I=16,200 \\
\end{align}\]
So, the total income is 16,200 rupees.
Now, let us calculate the angle for each item of expenditure by using the formula
\[\text{angle}=\dfrac{\text{amount spent on that item}}{\text{total income}}\times {{360}^{0}}\]
(i) Let us calculate angle for food
By using the above formula we get
\[\begin{align}
& \Rightarrow \text{angle of food}=\dfrac{3,750}{16,200}\times {{360}^{0}} \\
& \Rightarrow \text{angle of food}=83.34\simeq {{83}^{0}} \\
\end{align}\]
(ii) Let us calculate angle for health
By using the above formula we get
\[\begin{align}
& \Rightarrow \text{angle of health}=\dfrac{1,875}{16,200}\times {{360}^{0}} \\
& \Rightarrow \text{angle of clothing}=41.67\simeq {{42}^{0}} \\
\end{align}\]
(iii) Let us calculate angle for clothing
By using the above formula we get
\[\begin{align}
& \Rightarrow \text{angle of clothing}=\dfrac{1,875}{16,200}\times {{360}^{0}} \\
& \Rightarrow \text{angle of clothing}=41.67\simeq {{42}^{0}} \\
\end{align}\]
(iv) Let us calculate angle for education
By using the above formula we get
\[\begin{align}
& \Rightarrow \text{angle of education}=\dfrac{1,200}{16,200}\times {{360}^{0}} \\
& \Rightarrow \text{angle of education}=26.67\simeq {{27}^{0}} \\
\end{align}\]
(v) Let us calculate angle for savings
By using the above formula we get
\[\begin{align}
& \Rightarrow \text{angle of savings}=\dfrac{7,500}{16,200}\times {{360}^{0}} \\
& \Rightarrow \text{angle of savings}=166.34\simeq {{166}^{0}} \\
\end{align}\]
Now, by making these angles as parts in a circle we get a pie chart as
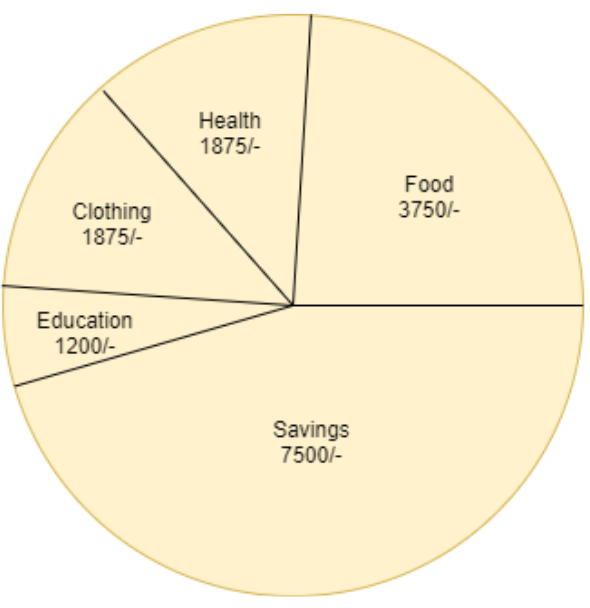
Note: Students may do mistake in following points
(i) We need to mention each part with its name.
(ii) Give each part to a certain design to avoid confusion
(iii) Angle should not be mentioned in the pie diagram but you can mention the amount spent.
Above mentioned points need to be taken care of while drawing the pie chart.
\[\text{angle}=\dfrac{\text{amount spent on that item}}{\text{total income}}\times {{360}^{0}}\]
After finding the angle for each item of expenditure we divide the circle corresponds to that angle and gives a name to each part.
Complete step-by-step solution:
Let us assume\[I\] be the income.
Let us find the total income by adding the amount spent on each item as
\[\begin{align}
& \Rightarrow I=3,750+1,875+1,875+1,200+7,500 \\
& \Rightarrow I=16,200 \\
\end{align}\]
So, the total income is 16,200 rupees.
Now, let us calculate the angle for each item of expenditure by using the formula
\[\text{angle}=\dfrac{\text{amount spent on that item}}{\text{total income}}\times {{360}^{0}}\]
(i) Let us calculate angle for food
By using the above formula we get
\[\begin{align}
& \Rightarrow \text{angle of food}=\dfrac{3,750}{16,200}\times {{360}^{0}} \\
& \Rightarrow \text{angle of food}=83.34\simeq {{83}^{0}} \\
\end{align}\]
(ii) Let us calculate angle for health
By using the above formula we get
\[\begin{align}
& \Rightarrow \text{angle of health}=\dfrac{1,875}{16,200}\times {{360}^{0}} \\
& \Rightarrow \text{angle of clothing}=41.67\simeq {{42}^{0}} \\
\end{align}\]
(iii) Let us calculate angle for clothing
By using the above formula we get
\[\begin{align}
& \Rightarrow \text{angle of clothing}=\dfrac{1,875}{16,200}\times {{360}^{0}} \\
& \Rightarrow \text{angle of clothing}=41.67\simeq {{42}^{0}} \\
\end{align}\]
(iv) Let us calculate angle for education
By using the above formula we get
\[\begin{align}
& \Rightarrow \text{angle of education}=\dfrac{1,200}{16,200}\times {{360}^{0}} \\
& \Rightarrow \text{angle of education}=26.67\simeq {{27}^{0}} \\
\end{align}\]
(v) Let us calculate angle for savings
By using the above formula we get
\[\begin{align}
& \Rightarrow \text{angle of savings}=\dfrac{7,500}{16,200}\times {{360}^{0}} \\
& \Rightarrow \text{angle of savings}=166.34\simeq {{166}^{0}} \\
\end{align}\]
Now, by making these angles as parts in a circle we get a pie chart as

Note: Students may do mistake in following points
(i) We need to mention each part with its name.
(ii) Give each part to a certain design to avoid confusion
(iii) Angle should not be mentioned in the pie diagram but you can mention the amount spent.
Above mentioned points need to be taken care of while drawing the pie chart.
Recently Updated Pages
What percentage of the area in India is covered by class 10 social science CBSE

The area of a 6m wide road outside a garden in all class 10 maths CBSE

What is the electric flux through a cube of side 1 class 10 physics CBSE

If one root of x2 x k 0 maybe the square of the other class 10 maths CBSE

The radius and height of a cylinder are in the ratio class 10 maths CBSE

An almirah is sold for 5400 Rs after allowing a discount class 10 maths CBSE

Trending doubts
The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

Why is there a time difference of about 5 hours between class 10 social science CBSE

Change the following sentences into negative and interrogative class 10 english CBSE

What constitutes the central nervous system How are class 10 biology CBSE

Write a letter to the principal requesting him to grant class 10 english CBSE

Explain the Treaty of Vienna of 1815 class 10 social science CBSE




