
Derive the relation between Focal length and radius of curvature for spherical mirrors.
Answer
543.3k+ views
Hint: Focal length and radius of curvature directly depends on each other. Focal length and radius of curvature for a mirror have the same unit. Also here we need to apply the rules or laws of reflection.
Complete step-by-step answer:
To find relation between focal length and radius of curvature for spherical mirror
Consider a concave mirror
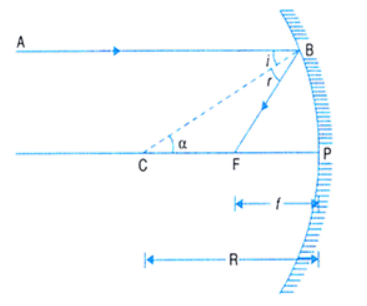
Where,
P = Pole, it is the midpoint of mirror
F = Focal point
C = center of curvature
Cp = Radius of creature
Ray parallel to principal axis strike at point A.
For Applying rules of reflection we have to draw a normal
As we know the line which strikes circular. Also we can say normal at the surface of the sphere will pass through the Center of curvature of mirror or spherical shapes.
Now According to Rules Angle of incident = Angle of Reflection
\[\angle i=\angle r\]
AS OA and OP are parallel to each other
\[\angle \text{ACE}=\text{ }i\text{ }\left( \text{Alternate Angle} \right)\text{ }..........\text{ 1}\]
Also \[\angle \text{FAC}=i\text{ }\left( \text{Reflection Angle} \right)~~~\text{ }\ldots \ldots \ldots \text{ }2\].
By equation 1 and 2
\[\angle \text{ACF}=\angle \text{FAS}=i\]
Therefore CF = FA
When incident way come closer to principal axis then FA= FP
Also we know CF = FP = f (focal length)
Then \[R=CP\]
\[=CF+FP\]
\[=F+F\]
\[=2F\]
So, Radius of curvature is double the focal length.
Note: The Principal focus of a spherical mirror lies in between the role and center of curvature. Also, the Radius of curvature is equal to twice of the focal length.
In general as we know we cut mirrors from the sphere. So the radius of that sphere from which the mirror has cut is known as the radius of curvature of the mirror. There is a focal point for every mirror. So focal length is defined as distance between focal point and mirror.
Complete step-by-step answer:
To find relation between focal length and radius of curvature for spherical mirror
Consider a concave mirror

Where,
P = Pole, it is the midpoint of mirror
F = Focal point
C = center of curvature
Cp = Radius of creature
Ray parallel to principal axis strike at point A.
For Applying rules of reflection we have to draw a normal
As we know the line which strikes circular. Also we can say normal at the surface of the sphere will pass through the Center of curvature of mirror or spherical shapes.
Now According to Rules Angle of incident = Angle of Reflection
\[\angle i=\angle r\]
AS OA and OP are parallel to each other
\[\angle \text{ACE}=\text{ }i\text{ }\left( \text{Alternate Angle} \right)\text{ }..........\text{ 1}\]
Also \[\angle \text{FAC}=i\text{ }\left( \text{Reflection Angle} \right)~~~\text{ }\ldots \ldots \ldots \text{ }2\].
By equation 1 and 2
\[\angle \text{ACF}=\angle \text{FAS}=i\]
Therefore CF = FA
When incident way come closer to principal axis then FA= FP
Also we know CF = FP = f (focal length)
Then \[R=CP\]
\[=CF+FP\]
\[=F+F\]
\[=2F\]
So, Radius of curvature is double the focal length.
Note: The Principal focus of a spherical mirror lies in between the role and center of curvature. Also, the Radius of curvature is equal to twice of the focal length.
In general as we know we cut mirrors from the sphere. So the radius of that sphere from which the mirror has cut is known as the radius of curvature of the mirror. There is a focal point for every mirror. So focal length is defined as distance between focal point and mirror.
Recently Updated Pages
Class 10 Question and Answer - Your Ultimate Solutions Guide

Master Class 10 Computer Science: Engaging Questions & Answers for Success

Master Class 10 Social Science: Engaging Questions & Answers for Success

Master Class 10 English: Engaging Questions & Answers for Success

Master Class 12 Chemistry: Engaging Questions & Answers for Success

Master Class 12 Biology: Engaging Questions & Answers for Success

Trending doubts
Why is there a time difference of about 5 hours between class 10 social science CBSE

Five things I will do to build a great India class 10 english CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

Fill the blanks with proper collective nouns 1 A of class 10 english CBSE

Select the word that is correctly spelled a Twelveth class 10 english CBSE

10 examples of evaporation in daily life with explanations




