
Derive the formula:- $n\left( {A \cup B \cup C} \right) = n\left( A \right) + n\left( B \right) + n\left( C \right) - n\left( {A \cap B} \right) - n\left( {B \cap C} \right) - n\left( {C \cap A} \right) + n\left( {A \cap B \cap C} \right)$
Answer
585k+ views
Hint: We know that for the sets A and B $n\left( {A \cup B} \right) = n\left( A \right) + n\left( B \right) - n\left( {A \cap B} \right)$ , where n(A) is the no. of elements in set A and n(B) is the no. of elements in set B and $n\left( {A \cup B} \right)$ is the no. of terms in the set A union B and $n\left( {A \cap B} \right)$ is the no. of elements in the set A intersection B. This formula is used when there are 2 sets. So use the same formula to solve for 3 sets by considering 2 sets as 1.
Complete step-by-step answer:
We are given to derive the formula $n\left( {A \cup B \cup C} \right) = n\left( A \right) + n\left( B \right) + n\left( C \right) - n\left( {A \cap B} \right) - n\left( {B \cap C} \right) - n\left( {C \cap A} \right) + n\left( {A \cap B \cap C} \right)$
Here A, B, C are three sets in the universe.
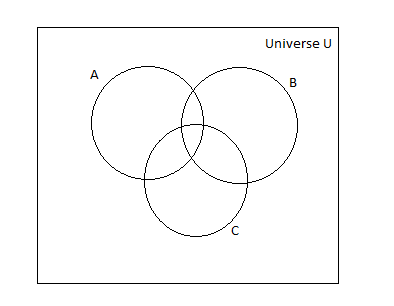
We know that $n\left( {A \cup B} \right) = n\left( A \right) + n\left( B \right) - n\left( {A \cap B} \right)$ for two sets A and B.
In $n\left( {A \cup B \cup C} \right)$ consider $A \cup B$ as one set and C as another set.
\[n\left( {A \cup B \cup C} \right) = n\left( {\left( {A \cup B} \right) \cup C} \right)\]
Substitute the value \[n\left( {A \cup B} \right) = n\left( A \right) + n\left( B \right) - n\left( {A \cap B} \right);A = A \cup B,B = C\] in the above expression
\[ = n\left( {A \cup B} \right) + n\left( C \right) - n\left( {\left( {A \cup B} \right) \cap C} \right)\]
Substitute the value of \[n\left( {A \cup B} \right) = n\left( A \right) + n\left( B \right) - n\left( {A \cap B} \right);A = A,B = B\] in the above expression
\[ = n\left( A \right) + n\left( B \right) - n\left( {A \cap B} \right) + n\left( C \right) - n\left( {\left( {A \cup B} \right) \cap C} \right)\]
The value of
\[\left( {A \cup B} \right) \cap C = \left( {A \cap C} \right) \cup \left( {B \cap C} \right)\] by distributive property.
\[ = n\left( A \right) + n\left( B \right) + n\left( C \right) - n\left( {A \cap B} \right) - n\left[ {\left( {A \cap C} \right) \cup \left( {B \cap C} \right)} \right]\]
Substitute the value \[n\left( {A \cup B} \right) = n\left( A \right) + n\left( B \right) - n\left( {A \cap B} \right);A = A \cap C,B = B \cap C\] in the above expression
\[
= n\left( A \right) + n\left( B \right) + n\left( C \right) - n\left( {A \cap B} \right) - \left( {n\left( {A \cap C} \right) + n\left( {B \cap C} \right) - n\left( {A \cap B \cap C} \right)} \right) \\
= n\left( A \right) + n\left( B \right) + n\left( C \right) - n\left( {A \cap B} \right) - n\left( {A \cap C} \right) - n\left( {B \cap C} \right) + n\left( {A \cap B \cap C} \right) \\
= n\left( A \right) + n\left( B \right) + n\left( C \right) - n\left( {A \cap B} \right) - n\left( {B \cap C} \right) - n\left( {A \cap C} \right) + n\left( {A \cap B \cap C} \right) \\
= n\left( A \right) + n\left( B \right) + n\left( C \right) - n\left( {A \cap B} \right) - n\left( {B \cap C} \right) - n\left( {C \cap A} \right) + n\left( {A \cap B \cap C} \right) \\
\]
The value of \[A \cap B = B \cap A\] by commutative property.
Therefore, the value of $n\left( {A \cup B \cup C} \right)$ is \[n\left( A \right) + n\left( B \right) + n\left( C \right) - n\left( {A \cap B} \right) - n\left( {B \cap C} \right) - n\left( {C \cap A} \right) + n\left( {A \cap B \cap C} \right)\]
Note: Sets are a well-defined collection of objects and can be represented in set-builder form or roster form. Sets are represented in curly braces {}. $ \cup $ is union and $ \cap $ is intersection. The union of two sets is a new set that contains all of the elements that are in at least one of the two sets whereas the intersection of two sets is a new set that contains all of the elements that are in both sets. So, do not confuse intersection with union.
Complete step-by-step answer:
We are given to derive the formula $n\left( {A \cup B \cup C} \right) = n\left( A \right) + n\left( B \right) + n\left( C \right) - n\left( {A \cap B} \right) - n\left( {B \cap C} \right) - n\left( {C \cap A} \right) + n\left( {A \cap B \cap C} \right)$
Here A, B, C are three sets in the universe.

We know that $n\left( {A \cup B} \right) = n\left( A \right) + n\left( B \right) - n\left( {A \cap B} \right)$ for two sets A and B.
In $n\left( {A \cup B \cup C} \right)$ consider $A \cup B$ as one set and C as another set.
\[n\left( {A \cup B \cup C} \right) = n\left( {\left( {A \cup B} \right) \cup C} \right)\]
Substitute the value \[n\left( {A \cup B} \right) = n\left( A \right) + n\left( B \right) - n\left( {A \cap B} \right);A = A \cup B,B = C\] in the above expression
\[ = n\left( {A \cup B} \right) + n\left( C \right) - n\left( {\left( {A \cup B} \right) \cap C} \right)\]
Substitute the value of \[n\left( {A \cup B} \right) = n\left( A \right) + n\left( B \right) - n\left( {A \cap B} \right);A = A,B = B\] in the above expression
\[ = n\left( A \right) + n\left( B \right) - n\left( {A \cap B} \right) + n\left( C \right) - n\left( {\left( {A \cup B} \right) \cap C} \right)\]
The value of
\[\left( {A \cup B} \right) \cap C = \left( {A \cap C} \right) \cup \left( {B \cap C} \right)\] by distributive property.
\[ = n\left( A \right) + n\left( B \right) + n\left( C \right) - n\left( {A \cap B} \right) - n\left[ {\left( {A \cap C} \right) \cup \left( {B \cap C} \right)} \right]\]
Substitute the value \[n\left( {A \cup B} \right) = n\left( A \right) + n\left( B \right) - n\left( {A \cap B} \right);A = A \cap C,B = B \cap C\] in the above expression
\[
= n\left( A \right) + n\left( B \right) + n\left( C \right) - n\left( {A \cap B} \right) - \left( {n\left( {A \cap C} \right) + n\left( {B \cap C} \right) - n\left( {A \cap B \cap C} \right)} \right) \\
= n\left( A \right) + n\left( B \right) + n\left( C \right) - n\left( {A \cap B} \right) - n\left( {A \cap C} \right) - n\left( {B \cap C} \right) + n\left( {A \cap B \cap C} \right) \\
= n\left( A \right) + n\left( B \right) + n\left( C \right) - n\left( {A \cap B} \right) - n\left( {B \cap C} \right) - n\left( {A \cap C} \right) + n\left( {A \cap B \cap C} \right) \\
= n\left( A \right) + n\left( B \right) + n\left( C \right) - n\left( {A \cap B} \right) - n\left( {B \cap C} \right) - n\left( {C \cap A} \right) + n\left( {A \cap B \cap C} \right) \\
\]
The value of \[A \cap B = B \cap A\] by commutative property.
Therefore, the value of $n\left( {A \cup B \cup C} \right)$ is \[n\left( A \right) + n\left( B \right) + n\left( C \right) - n\left( {A \cap B} \right) - n\left( {B \cap C} \right) - n\left( {C \cap A} \right) + n\left( {A \cap B \cap C} \right)\]
Note: Sets are a well-defined collection of objects and can be represented in set-builder form or roster form. Sets are represented in curly braces {}. $ \cup $ is union and $ \cap $ is intersection. The union of two sets is a new set that contains all of the elements that are in at least one of the two sets whereas the intersection of two sets is a new set that contains all of the elements that are in both sets. So, do not confuse intersection with union.
Recently Updated Pages
Master Class 8 Social Science: Engaging Questions & Answers for Success

Master Class 8 English: Engaging Questions & Answers for Success

Class 8 Question and Answer - Your Ultimate Solutions Guide

Master Class 8 Maths: Engaging Questions & Answers for Success

Master Class 8 Science: Engaging Questions & Answers for Success

Master Class 7 English: Engaging Questions & Answers for Success

Trending doubts
Which are the Top 10 Largest States of India?

What is the theme or message of the poem The road not class 9 english CBSE

What are the major achievements of the UNO class 9 social science CBSE

Explain the importance of pH in everyday life class 9 chemistry CBSE

Differentiate between parenchyma collenchyma and sclerenchyma class 9 biology CBSE

Give 5 examples of refraction of light in daily life




