
Derive the formula for equivalent capacitance when the capacitors are connected in series.
Answer
518.1k+ views
Hint
Two conducting plates separated by a distance is called a capacitor. On the application of current, the plates will get charged with the opposite charge. In a series connection, the capacitors are connected in an end to end connection. In a series connection, each capacitor will carry the same amount of charge.
Complete step by step answer
Consider a series combination of capacitors, where the capacitors are connected in an end to end connection as shown in the figure.
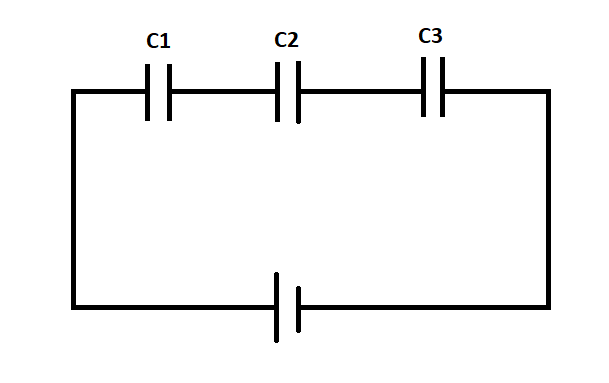
Let $ V $ be the potential difference applied across the series combination. The one property that we have to take care of in a series combination is that each capacitor will have the same amount of charge.
Let the potential difference be, $ {V_1},{V_2} $ and $ {V_3} $ across the capacitors, $ {C_1},{C_2} $ and $ {C_3} $ respectively,
$ \therefore $ We can write the applied potential as,
$\Rightarrow V = {V_1} + {V_2} + {V_3} $
The potential difference of each capacitor can be written as,
$\Rightarrow {V_1} = \dfrac{{{Q_1}}}{{{C_1}}},{V_2} = \dfrac{{{Q_2}}}{{{C_2}}} $ and $ {V_3} = \dfrac{{{Q_3}}}{{{C_3}}} $
If we replace the combination of capacitors with a single capacitor, then we can write the effective resistance as,
$\Rightarrow V = \dfrac{Q}{C} $
Substituting equation and in equation we get,
$\Rightarrow \dfrac{Q}{C} = \left[ {\dfrac{{{Q_1}}}{{{C_1}}} + \dfrac{{{Q_2}}}{{{C_2}}} + \dfrac{{{Q_3}}}{{{C_3}}}} \right] $
From this we get the effective capacitance as,
$\Rightarrow \dfrac{1}{C} = \dfrac{1}{{{C_1}}} + \dfrac{1}{{{C_2}}} + \dfrac{1}{{{C_3}}} $
Thus we get that, the reciprocal of the effective capacitance is equal to the sum of the reciprocal of the individual capacitances.
Note
In a series combination, the effective capacitance will be less than the lowest capacitance in the combination. Thus a series combination is used to reduce the effective capacitance. The effective capacitance in a parallel combination is higher than the highest value of capacitance in the combination. Thus a parallel combination is used to increase the effective capacitance of the circuit.
Two conducting plates separated by a distance is called a capacitor. On the application of current, the plates will get charged with the opposite charge. In a series connection, the capacitors are connected in an end to end connection. In a series connection, each capacitor will carry the same amount of charge.
Complete step by step answer
Consider a series combination of capacitors, where the capacitors are connected in an end to end connection as shown in the figure.

Let $ V $ be the potential difference applied across the series combination. The one property that we have to take care of in a series combination is that each capacitor will have the same amount of charge.
Let the potential difference be, $ {V_1},{V_2} $ and $ {V_3} $ across the capacitors, $ {C_1},{C_2} $ and $ {C_3} $ respectively,
$ \therefore $ We can write the applied potential as,
$\Rightarrow V = {V_1} + {V_2} + {V_3} $
The potential difference of each capacitor can be written as,
$\Rightarrow {V_1} = \dfrac{{{Q_1}}}{{{C_1}}},{V_2} = \dfrac{{{Q_2}}}{{{C_2}}} $ and $ {V_3} = \dfrac{{{Q_3}}}{{{C_3}}} $
If we replace the combination of capacitors with a single capacitor, then we can write the effective resistance as,
$\Rightarrow V = \dfrac{Q}{C} $
Substituting equation and in equation we get,
$\Rightarrow \dfrac{Q}{C} = \left[ {\dfrac{{{Q_1}}}{{{C_1}}} + \dfrac{{{Q_2}}}{{{C_2}}} + \dfrac{{{Q_3}}}{{{C_3}}}} \right] $
From this we get the effective capacitance as,
$\Rightarrow \dfrac{1}{C} = \dfrac{1}{{{C_1}}} + \dfrac{1}{{{C_2}}} + \dfrac{1}{{{C_3}}} $
Thus we get that, the reciprocal of the effective capacitance is equal to the sum of the reciprocal of the individual capacitances.
Note
In a series combination, the effective capacitance will be less than the lowest capacitance in the combination. Thus a series combination is used to reduce the effective capacitance. The effective capacitance in a parallel combination is higher than the highest value of capacitance in the combination. Thus a parallel combination is used to increase the effective capacitance of the circuit.
Recently Updated Pages
Master Class 12 Biology: Engaging Questions & Answers for Success

Master Class 12 Physics: Engaging Questions & Answers for Success

Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Trending doubts
Which are the Top 10 Largest Countries of the World?

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE

Why is the cell called the structural and functional class 12 biology CBSE

a Tabulate the differences in the characteristics of class 12 chemistry CBSE

Who discovered the cell and how class 12 biology CBSE

Draw a labelled sketch of the human eye class 12 physics CBSE




