
Convert ${{40}^{\circ }}{{20}^{'}}$ into radian. \[\]
Answer
537k+ views
Hint: We recall the definitions of degree and radian as the units to measure angles. We use the formula $R=\dfrac{\pi D}{180}$ to convert from degree to radian where D is the measure of angle in degree and R is the measure of angle in radian.
Complete step-by-step answer:
We know that degree is a unit for measurement of angle in a plane . If D is the measurement of the angle and it is denoted in degree with a small circle superscript $'\circ '$ as ${{D}^{\circ }}$. One degree is equal to the angle subtended at the centre by an arc of length equal to $\dfrac{1}{360}$ of circle. A degree is further divided into minutes and seconds. 1 degree is equal to 60 minutes and 1minuite is equal to 60 seconds. \[\]
We also know that radian is the standard unit for measurement of angle in plane. If R is the measurement of the angle and it is denoted in radian with a small ‘c’ superscript symbol as ${{R}^{c}}$.1 radian is equal to the measure of angle made at the centre of a circle by an arc whose length is equal to the radius of the circle.\[\]
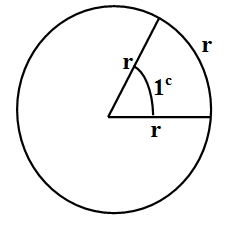
We convert the equal measures ${{R}^{c}}$ and ${{D}^{\circ }}$into other units using fowling formulae.
\[\begin{align}
& {{D}^{\circ }}=\dfrac{180}{\pi }\times {{R}^{c}} \\
& {{R}^{c}}=\dfrac{\pi }{180}\times {{D}^{\circ }} \\
\end{align}\]
We are asked to convert the given measure of an angle in degree ${{40}^{\circ }}{{20}^{'}}$ into radian. Let us first convert the given measure in degree and minutes into fractions.
We know that ${{60}^{'}}$ minute is ${{1}^{\circ }}$, then ${{1}^{'}}$ is ${{\left( \dfrac{1}{60} \right)}^{\circ }}$ and then ${{20}^{'}}$ in degree is ${{\left( 20\times \dfrac{1}{60} \right)}^{\circ }}={{\left( \dfrac{1}{3} \right)}^{\circ }}$. So the measure ${{40}^{\circ }}{{20}^{'}}$ in fraction is ${{40}^{\circ }}+{{\left( \dfrac{1}{3} \right)}^{\circ }}={{\left( \dfrac{120+1}{3} \right)}^{\circ }}={{\left( \dfrac{121}{3} \right)}^{\circ }}$
Now we use the formula for converting degrees into radian where $D=\dfrac{121}{3}$. We have;
\[{{R}^{c}}=\dfrac{\pi }{180}\times {{D}^{\circ }}=\dfrac{\pi }{180}\times \dfrac{121}{3}={{\left( \dfrac{121}{540}\pi \right)}^{c}}\]
The measure of angle in radian is ${{\left( \dfrac{121}{540}\pi \right)}^{c}}$.\[\]
Note: We have used the unitary method for direct variation to convert ${{20}^{'}}$ into degree. We note that a circular angle or complete angle is measured in ${{360}^{\circ }}$ or $2{{\pi }^{c}}$. So we use unitary method for direct variation we have ${{360}^{\circ }}=2{{\pi }^{c}}\Rightarrow {{1}^{\circ }}={{\left( \dfrac{\pi }{180} \right)}^{c}},{{360}^{\circ }}=2{{\pi }^{c}}\Rightarrow {{1}^{c}}={{\left( \dfrac{180}{\pi } \right)}^{\circ }}$ . Another unit of measure of angle is gradians (gons) which measures the complete angle as ${{400}^{g}}$.
Complete step-by-step answer:
We know that degree is a unit for measurement of angle in a plane . If D is the measurement of the angle and it is denoted in degree with a small circle superscript $'\circ '$ as ${{D}^{\circ }}$. One degree is equal to the angle subtended at the centre by an arc of length equal to $\dfrac{1}{360}$ of circle. A degree is further divided into minutes and seconds. 1 degree is equal to 60 minutes and 1minuite is equal to 60 seconds. \[\]
We also know that radian is the standard unit for measurement of angle in plane. If R is the measurement of the angle and it is denoted in radian with a small ‘c’ superscript symbol as ${{R}^{c}}$.1 radian is equal to the measure of angle made at the centre of a circle by an arc whose length is equal to the radius of the circle.\[\]

We convert the equal measures ${{R}^{c}}$ and ${{D}^{\circ }}$into other units using fowling formulae.
\[\begin{align}
& {{D}^{\circ }}=\dfrac{180}{\pi }\times {{R}^{c}} \\
& {{R}^{c}}=\dfrac{\pi }{180}\times {{D}^{\circ }} \\
\end{align}\]
We are asked to convert the given measure of an angle in degree ${{40}^{\circ }}{{20}^{'}}$ into radian. Let us first convert the given measure in degree and minutes into fractions.
We know that ${{60}^{'}}$ minute is ${{1}^{\circ }}$, then ${{1}^{'}}$ is ${{\left( \dfrac{1}{60} \right)}^{\circ }}$ and then ${{20}^{'}}$ in degree is ${{\left( 20\times \dfrac{1}{60} \right)}^{\circ }}={{\left( \dfrac{1}{3} \right)}^{\circ }}$. So the measure ${{40}^{\circ }}{{20}^{'}}$ in fraction is ${{40}^{\circ }}+{{\left( \dfrac{1}{3} \right)}^{\circ }}={{\left( \dfrac{120+1}{3} \right)}^{\circ }}={{\left( \dfrac{121}{3} \right)}^{\circ }}$
Now we use the formula for converting degrees into radian where $D=\dfrac{121}{3}$. We have;
\[{{R}^{c}}=\dfrac{\pi }{180}\times {{D}^{\circ }}=\dfrac{\pi }{180}\times \dfrac{121}{3}={{\left( \dfrac{121}{540}\pi \right)}^{c}}\]
The measure of angle in radian is ${{\left( \dfrac{121}{540}\pi \right)}^{c}}$.\[\]
Note: We have used the unitary method for direct variation to convert ${{20}^{'}}$ into degree. We note that a circular angle or complete angle is measured in ${{360}^{\circ }}$ or $2{{\pi }^{c}}$. So we use unitary method for direct variation we have ${{360}^{\circ }}=2{{\pi }^{c}}\Rightarrow {{1}^{\circ }}={{\left( \dfrac{\pi }{180} \right)}^{c}},{{360}^{\circ }}=2{{\pi }^{c}}\Rightarrow {{1}^{c}}={{\left( \dfrac{180}{\pi } \right)}^{\circ }}$ . Another unit of measure of angle is gradians (gons) which measures the complete angle as ${{400}^{g}}$.
Recently Updated Pages
Percolation tank is constructed to impound A Runoff class 10 biology CBSE

If a2 + b2 + c2 + 3 2a + b + c then the value of a class 10 maths CBSE

Fill up with a suitable word from the given options class 10 english CBSE

Tangent and normal to the curve y2sin x+sin 2xare drawn class 10 maths CBSE

There is a hexagon MNOPQR of each side 5cm and symmetric class 10 maths CBSE

What should be the maximum permissible strength of class 10 social science CBSE

Trending doubts
Write an application to the principal requesting five class 10 english CBSE

Why is there a time difference of about 5 hours between class 10 social science CBSE

Write a letter to the principal requesting him to grant class 10 english CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

What is the median of the first 10 natural numbers class 10 maths CBSE

Write examples of herbivores carnivores and omnivo class 10 biology CBSE




