
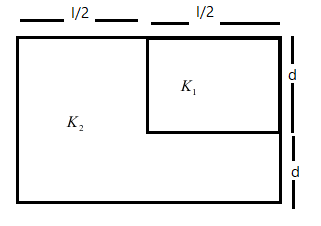
What is the capacitance of the capacitor of square plates of area $A$, shown in the figure

Answer
511.8k+ views
Hint: A capacitor is a two terminal component that stores electrical energy in the form of potential energy, and later discharges them. This property is called the capacitance of the capacitor. The capacitors can be connected in series or in parallel with respect to each other.
Formula:
$C=\dfrac{KA\epsilon_{0}}{d}$
Complete step by step answer:
A capacitor can store electrical energy, and behaves as a temporary battery. They are used mainly to maintain the power supply while batteries are being changed. It can also store information in the form of binary digits. It is the main component used in full wave and half wave rectifiers. (symbol: F), named after the English physicist Michael Faraday. A 1 farad capacitor, when charged with 1 coulomb of electrical charge, has a potential difference of 1 volt between its plates.
We know that the charge $Q$ produced due to capacitance $C$ and potential difference $V$ is given as $Q=CV$. Also, the energy of the capacitor is $E=\dfrac{1}{2}CV^{2}$.
We know that $C=\dfrac{KA\epsilon_{0}}{d}$ where, $A$ is the area of the capacitance and $d$ is the width of the dielectric $K$and the electric constant $\epsilon_{0}=8.854\times 10^{-12}Fm^{-1}$
Here, we have a capacitance$C_{1}$ filled with $K_{1}$, then, $C_{1}=\dfrac{K_{1}d\epsilon_{0}}{d}\times\dfrac{l}{2}=\dfrac{K_{1}\epsilon_{0}l}{2}$
Similarly, we have a capacitance $C_{2}$ is filled with $K_{2}$, then, we can divide the capacitance into two areas, then we have the following $C_{2}=\dfrac{K_{2}\epsilon_{0}ld}{2\left(\dfrac{l}{2}\right)}+\dfrac{K_{2}\epsilon_{0}ld}{2d}$
$\implies C_{2}=K_{2}\epsilon_{0}d+\dfrac{K_{2}\epsilon_{0}ld}{2}$
$\therefore C_{2}=K_{2}\epsilon_{0}d\left(1+\dfrac{l}{2}\right)$
Then the net $C=C_{1}+C_{2}=\dfrac{K_{1}\epsilon_{0}l}{2}+K_{2}\epsilon_{0}d\left(1+\dfrac{l}{2}\right)$
Note:
The series of capacitors is the sum of reciprocal of its individual capacitors, whereas in resistance the parallel is the sum of reciprocal of its individual resistors. Also remember that capacitors can charge and discharge. To solve the question, we can divide the given area into small capacitance.
Formula:
$C=\dfrac{KA\epsilon_{0}}{d}$
Complete step by step answer:
A capacitor can store electrical energy, and behaves as a temporary battery. They are used mainly to maintain the power supply while batteries are being changed. It can also store information in the form of binary digits. It is the main component used in full wave and half wave rectifiers. (symbol: F), named after the English physicist Michael Faraday. A 1 farad capacitor, when charged with 1 coulomb of electrical charge, has a potential difference of 1 volt between its plates.
We know that the charge $Q$ produced due to capacitance $C$ and potential difference $V$ is given as $Q=CV$. Also, the energy of the capacitor is $E=\dfrac{1}{2}CV^{2}$.
We know that $C=\dfrac{KA\epsilon_{0}}{d}$ where, $A$ is the area of the capacitance and $d$ is the width of the dielectric $K$and the electric constant $\epsilon_{0}=8.854\times 10^{-12}Fm^{-1}$
Here, we have a capacitance$C_{1}$ filled with $K_{1}$, then, $C_{1}=\dfrac{K_{1}d\epsilon_{0}}{d}\times\dfrac{l}{2}=\dfrac{K_{1}\epsilon_{0}l}{2}$
Similarly, we have a capacitance $C_{2}$ is filled with $K_{2}$, then, we can divide the capacitance into two areas, then we have the following $C_{2}=\dfrac{K_{2}\epsilon_{0}ld}{2\left(\dfrac{l}{2}\right)}+\dfrac{K_{2}\epsilon_{0}ld}{2d}$
$\implies C_{2}=K_{2}\epsilon_{0}d+\dfrac{K_{2}\epsilon_{0}ld}{2}$
$\therefore C_{2}=K_{2}\epsilon_{0}d\left(1+\dfrac{l}{2}\right)$
Then the net $C=C_{1}+C_{2}=\dfrac{K_{1}\epsilon_{0}l}{2}+K_{2}\epsilon_{0}d\left(1+\dfrac{l}{2}\right)$
Note:
The series of capacitors is the sum of reciprocal of its individual capacitors, whereas in resistance the parallel is the sum of reciprocal of its individual resistors. Also remember that capacitors can charge and discharge. To solve the question, we can divide the given area into small capacitance.
Recently Updated Pages
Master Class 12 Biology: Engaging Questions & Answers for Success

Master Class 12 Physics: Engaging Questions & Answers for Success

Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 11 Social Science: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Trending doubts
Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE

Which are the Top 10 Largest Countries of the World?

Why is the cell called the structural and functional class 12 biology CBSE

a Tabulate the differences in the characteristics of class 12 chemistry CBSE

Pomato is a Somatic hybrid b Allopolyploid c Natural class 12 biology CBSE

Who discovered the cell and how class 12 biology CBSE




