
At what time between \[2\] o’ clock and \[3\] o’ clock will the two hands be opposite?
Answer
423k+ views
Hint: A clock has two hands, the smaller one is called the hour hand or shorthand while the large one is called the minute hand or long hand. Angle traced by hour hand in \[12\] hour is \[360^\circ \] . Angle traced by minute hand in \[60\] minutes is \[360^\circ \]. When the hour hand and minute hand are at \[180^\circ \] angle with each other, the hands are in opposite directions. When they are in opposite directions, they are \[30\] minutes spaces apart which means the hour hand is \[30\] minutes spaces ahead or behind the minute hand or the minute hand is \[30\] minutes spaces ahead or behind the hour hand. In \[60\] minutes, the minute hand gains \[55\] minutes on the hour hand which means in \[60\] minutes hour hand moves \[5\] minutes spaces ahead while the minute hand moves \[60\] minutes spaces.
Complete step by step answer:
At \[2\] o’ clock the minute hand points at \[12\] and the hour hand points at \[2\] of the clock. Hence, at \[2\] o’ clock the minute hand is \[10\] minutes behind the hour hand. Now, when the two hands are in opposite directions, they are \[30\] minutes apart. To be in the same straight line but not together they will be \[30\] minutes spaces apart .
So , the minute hand will have to gain \[(30 + 10) = 40\] minutes spaces over the hour hand which means the minute hand needs to gain \[40\] minutes spaces to be \[30\] minutes spaces ahead of the hour hand. We know, \[55\] minutes spaces are gained in \[60\] minutes and \[40\] minutes spaces are gained in \[\dfrac{{60}}{{55}} \times 40 = 43\dfrac{7}{{11}}\] minutes. The hand will be in the opposite direction at \[43\dfrac{7}{{11}}\] minutes past \[2\].
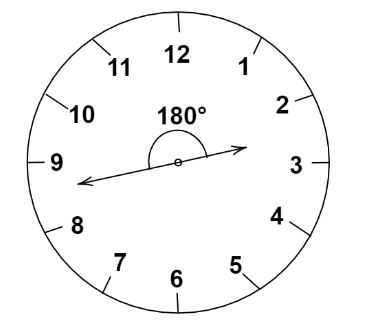
Note: In this question , to be in the opposite direction the minute hand has to be \[30\] minutes ahead of the hour hand. The hands of the clock point in opposite directions (in the same straight line) \[11\] times in twelve hours. So in a day, the hands point in the opposite direction \[22\] times. In this sum we have applied a unitary method to find the required answer.
Complete step by step answer:
At \[2\] o’ clock the minute hand points at \[12\] and the hour hand points at \[2\] of the clock. Hence, at \[2\] o’ clock the minute hand is \[10\] minutes behind the hour hand. Now, when the two hands are in opposite directions, they are \[30\] minutes apart. To be in the same straight line but not together they will be \[30\] minutes spaces apart .
So , the minute hand will have to gain \[(30 + 10) = 40\] minutes spaces over the hour hand which means the minute hand needs to gain \[40\] minutes spaces to be \[30\] minutes spaces ahead of the hour hand. We know, \[55\] minutes spaces are gained in \[60\] minutes and \[40\] minutes spaces are gained in \[\dfrac{{60}}{{55}} \times 40 = 43\dfrac{7}{{11}}\] minutes. The hand will be in the opposite direction at \[43\dfrac{7}{{11}}\] minutes past \[2\].

Note: In this question , to be in the opposite direction the minute hand has to be \[30\] minutes ahead of the hour hand. The hands of the clock point in opposite directions (in the same straight line) \[11\] times in twelve hours. So in a day, the hands point in the opposite direction \[22\] times. In this sum we have applied a unitary method to find the required answer.
Recently Updated Pages
Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Social Science: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Master Class 11 Physics: Engaging Questions & Answers for Success

Trending doubts
Difference Between Plant Cell and Animal Cell

Name 10 Living and Non living things class 9 biology CBSE

Fill the blanks with the suitable prepositions 1 The class 9 english CBSE

The highest mountain peak in India is A Kanchenjunga class 9 social science CBSE

On an outline map of India show its neighbouring c class 9 social science CBSE

Write the 6 fundamental rights of India and explain in detail




