
A tree breaks due to a storm and the broken part bends so that the top of the tree touches the ground by making \[30{}^\circ \] angle with the ground. The distance between the foot of the tree and the top of the tree on the ground is 6 meters. Find the height of the tree before falling.
Answer
561.9k+ views
Hint: Assume that the height of the tree is AB and C is the point at which the tree is broken is x m high from the ground. In \[\Delta CBA\] , we have Perpendicular = \[CB=BC=x\] and Base = \[AB=6\] . We know the formula of tan ratio in a triangle, \[\tan \theta =\dfrac{Perpendicular}{Base}\] . Now, apply the tan ratio in \[\Delta CBA\] . Now, solve it further and get the value of x using \[\tan 30{}^\circ =\dfrac{1}{\sqrt{3}}\] . Now, use the Pythagoras theorem, \[{{\left( Hypotenuse \right)}^{2}}={{\left( Perpendicular \right)}^{2}}+{{\left( Base \right)}^{2}}\] and calculate the value of the hypotenuse, CA. The height of the tree is AB, \[AB=BC+CA\] . Now, get the height AB.
Complete step-by-step answer:
First of all, let us assume that the height of the tree is AB and C is the point at which the tree is broken is x m high from the ground.
It is given that the total height of the tree is 6 meters and the top of the tree touches the ground by making \[30{}^\circ \] angle with the ground.
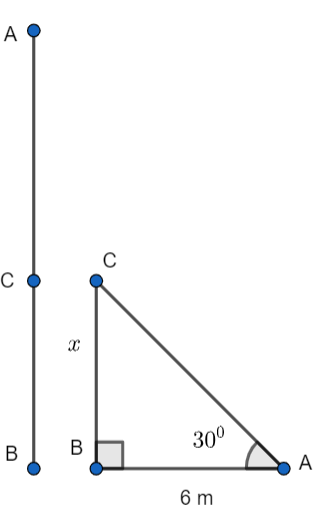
The distance between the foot of the tree and the top of the tree on the ground, AB = 6 meters
………………………………………(1)
The height from the ground at which the tree is broken, BC = x meters ……………………………….(2)
Now, in \[\Delta CBA\], we have
Perpendicular = \[CB=BC=x\] (from equation (2))
Base = \[AB=6\] (from equation (1))
\[\angle CAB=30{}^\circ \] (given)
We know the formula of tan ratio in a triangle, \[\tan \theta =\dfrac{Perpendicular}{Base}\] .
Applying the tan ratio in \[\Delta CBA\] , we get
\[\tan \theta =\dfrac{Perpendicular}{Base}\] ……………………………(3)
From equation (1) and equation (2), we have the values of the base and the perpendicular respectively.
Now, putting the value of the perpendicular and the base in equation (5), we get
\[\Rightarrow \tan 30{}^\circ =\dfrac{x}{6}\] …………………………(4)
We know that, \[\tan 30{}^\circ =\dfrac{1}{\sqrt{3}}\] ……………………(5)
From equation (4) and equation (5), we get
\[\begin{align}
& \Rightarrow \dfrac{1}{\sqrt{3}}=\dfrac{x}{6} \\
& \Rightarrow 6=\sqrt{3}x \\
& \Rightarrow \dfrac{6}{\sqrt{3}}=x \\
\end{align}\]
\[\Rightarrow 2\sqrt{3}=x\] ………………………(6)
Putting, the value of x from equation (6) in equation (2), we get
Perpendicular = \[CB=BC=2\sqrt{3}\]
So, the height at which the tree is broken is \[2\sqrt{3}\] meters high.
In the \[\Delta CBA\], we have
Perpendicular= CA = \[2\sqrt{3}\] meters …………………………(7)
Base = BC = 6 meters …………………………………..(8)
Hypotenuse = CA ……………………………………..(9)
\[\angle CBA=90{}^\circ \]
Since \[\Delta CBA\] is a right-angled triangle, we can apply Pythagoras theorem here.
We know the Pythagoras theorem,
\[{{\left( Hypotenuse \right)}^{2}}={{\left( Perpendicular \right)}^{2}}+{{\left( Base \right)}^{2}}\] ………………………………..(10)
Now, from equation (7), equation (8), equation (9), and equation (10), we get
\[\begin{align}
& \Rightarrow {{\left( CA \right)}^{2}}={{\left( 2\sqrt{3} \right)}^{2}}+{{\left( 6 \right)}^{2}} \\
& \Rightarrow {{\left( CA \right)}^{2}}=12+36 \\
& \Rightarrow {{\left( CA \right)}^{2}}=48 \\
& \Rightarrow CA=\sqrt{48} \\
\end{align}\]
\[\Rightarrow CA=4\sqrt{3}\] …………………………………(11)
In the figure, we can see that the height AB is the summation of the length BC and CA.
So, \[AB=BC+CA\] ……………………………………(12)
Now, from equation (7), equation (8), equation (11), and equation (12), we get
\[\Rightarrow AB=2\sqrt{3}+4\sqrt{3}=6\sqrt{3}\] …………………………………..(13)
Therefore, the height of the tree is \[6\sqrt{3}\] meters.
Note: We can also solve this question using the projection formula.
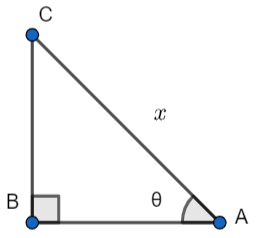
Here in this figure, the length AB is the projection of the length AC and \[\theta \] is the projection angle.
AB can be written as, \[AB=AC\times \cos \theta \] ………………………(1)
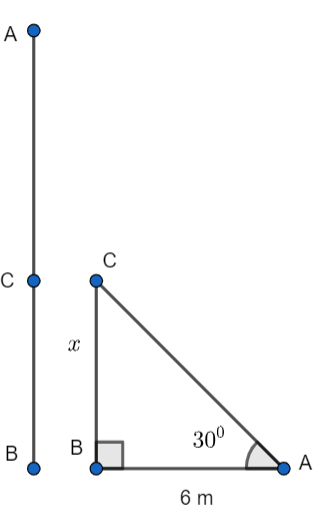
Now, in the \[\Delta CBA\] , we have
AB = 6 …………………………..(2)
\[\angle CAB=30{}^\circ \] ……………………….(3)
The side AB is the projection of the side AC and \[30{}^\circ \] is the angle of projection.
Now, using equation (1), we can say that \[6=AC\times \cos 30{}^\circ \] …………..…………….(4)
We know that, \[\cos 30{}^\circ =\dfrac{\sqrt{3}}{2}\] …………………………..(5)
Now, from equation (4) and equation (5), we get
\[\begin{align}
& \Rightarrow 6=AC\times \dfrac{\sqrt{3}}{2} \\
& \Rightarrow \dfrac{12}{\sqrt{3}}=AC \\
\end{align}\]
\[\Rightarrow 4\sqrt{3}=AC\] …………………………………(6)
In the \[\Delta CBA\] , we have \[\angle CBA=90{}^\circ \] .
Since \[\Delta CBA\] is a right-angled triangle so, we can apply Pythagoras theorem here.
We know the Pythagoras theorem,
\[{{\left( Hypotenuse \right)}^{2}}={{\left( Perpendicular \right)}^{2}}+{{\left( Base \right)}^{2}}\] ………………………………..(7)
Now, from equation (2), equation (6), and equation (7), we get
\[\begin{align}
& \Rightarrow {{\left( 4\sqrt{3} \right)}^{2}}={{\left( BC \right)}^{2}}+{{\left( 6 \right)}^{2}} \\
& \Rightarrow 48={{\left( BC \right)}^{2}}+36 \\
& \Rightarrow 48-36={{\left( BC \right)}^{2}} \\
& \Rightarrow 12={{\left( BC \right)}^{2}} \\
& \Rightarrow \sqrt{12}=BC \\
\end{align}\]
\[\Rightarrow 2\sqrt{3}=BC\] ………………………………..(8)
In the figure, we can see that the height AB is the summation of the length BC and CA.
So, \[AB=BC+CA\] ………………………………..(9)
From equation (6), equation (8), and equation (9), we get
\[\Rightarrow AB=2\sqrt{3}+4\sqrt{3}=6\sqrt{3}\]
Therefore, the height of the tree is \[6\sqrt{3}\] meters.
Complete step-by-step answer:
First of all, let us assume that the height of the tree is AB and C is the point at which the tree is broken is x m high from the ground.
It is given that the total height of the tree is 6 meters and the top of the tree touches the ground by making \[30{}^\circ \] angle with the ground.

The distance between the foot of the tree and the top of the tree on the ground, AB = 6 meters
………………………………………(1)
The height from the ground at which the tree is broken, BC = x meters ……………………………….(2)
Now, in \[\Delta CBA\], we have
Perpendicular = \[CB=BC=x\] (from equation (2))
Base = \[AB=6\] (from equation (1))
\[\angle CAB=30{}^\circ \] (given)
We know the formula of tan ratio in a triangle, \[\tan \theta =\dfrac{Perpendicular}{Base}\] .
Applying the tan ratio in \[\Delta CBA\] , we get
\[\tan \theta =\dfrac{Perpendicular}{Base}\] ……………………………(3)
From equation (1) and equation (2), we have the values of the base and the perpendicular respectively.
Now, putting the value of the perpendicular and the base in equation (5), we get
\[\Rightarrow \tan 30{}^\circ =\dfrac{x}{6}\] …………………………(4)
We know that, \[\tan 30{}^\circ =\dfrac{1}{\sqrt{3}}\] ……………………(5)
From equation (4) and equation (5), we get
\[\begin{align}
& \Rightarrow \dfrac{1}{\sqrt{3}}=\dfrac{x}{6} \\
& \Rightarrow 6=\sqrt{3}x \\
& \Rightarrow \dfrac{6}{\sqrt{3}}=x \\
\end{align}\]
\[\Rightarrow 2\sqrt{3}=x\] ………………………(6)
Putting, the value of x from equation (6) in equation (2), we get
Perpendicular = \[CB=BC=2\sqrt{3}\]
So, the height at which the tree is broken is \[2\sqrt{3}\] meters high.
In the \[\Delta CBA\], we have
Perpendicular= CA = \[2\sqrt{3}\] meters …………………………(7)
Base = BC = 6 meters …………………………………..(8)
Hypotenuse = CA ……………………………………..(9)
\[\angle CBA=90{}^\circ \]
Since \[\Delta CBA\] is a right-angled triangle, we can apply Pythagoras theorem here.
We know the Pythagoras theorem,
\[{{\left( Hypotenuse \right)}^{2}}={{\left( Perpendicular \right)}^{2}}+{{\left( Base \right)}^{2}}\] ………………………………..(10)
Now, from equation (7), equation (8), equation (9), and equation (10), we get
\[\begin{align}
& \Rightarrow {{\left( CA \right)}^{2}}={{\left( 2\sqrt{3} \right)}^{2}}+{{\left( 6 \right)}^{2}} \\
& \Rightarrow {{\left( CA \right)}^{2}}=12+36 \\
& \Rightarrow {{\left( CA \right)}^{2}}=48 \\
& \Rightarrow CA=\sqrt{48} \\
\end{align}\]
\[\Rightarrow CA=4\sqrt{3}\] …………………………………(11)
In the figure, we can see that the height AB is the summation of the length BC and CA.
So, \[AB=BC+CA\] ……………………………………(12)
Now, from equation (7), equation (8), equation (11), and equation (12), we get
\[\Rightarrow AB=2\sqrt{3}+4\sqrt{3}=6\sqrt{3}\] …………………………………..(13)
Therefore, the height of the tree is \[6\sqrt{3}\] meters.
Note: We can also solve this question using the projection formula.

Here in this figure, the length AB is the projection of the length AC and \[\theta \] is the projection angle.
AB can be written as, \[AB=AC\times \cos \theta \] ………………………(1)

Now, in the \[\Delta CBA\] , we have
AB = 6 …………………………..(2)
\[\angle CAB=30{}^\circ \] ……………………….(3)
The side AB is the projection of the side AC and \[30{}^\circ \] is the angle of projection.
Now, using equation (1), we can say that \[6=AC\times \cos 30{}^\circ \] …………..…………….(4)
We know that, \[\cos 30{}^\circ =\dfrac{\sqrt{3}}{2}\] …………………………..(5)
Now, from equation (4) and equation (5), we get
\[\begin{align}
& \Rightarrow 6=AC\times \dfrac{\sqrt{3}}{2} \\
& \Rightarrow \dfrac{12}{\sqrt{3}}=AC \\
\end{align}\]
\[\Rightarrow 4\sqrt{3}=AC\] …………………………………(6)
In the \[\Delta CBA\] , we have \[\angle CBA=90{}^\circ \] .
Since \[\Delta CBA\] is a right-angled triangle so, we can apply Pythagoras theorem here.
We know the Pythagoras theorem,
\[{{\left( Hypotenuse \right)}^{2}}={{\left( Perpendicular \right)}^{2}}+{{\left( Base \right)}^{2}}\] ………………………………..(7)
Now, from equation (2), equation (6), and equation (7), we get
\[\begin{align}
& \Rightarrow {{\left( 4\sqrt{3} \right)}^{2}}={{\left( BC \right)}^{2}}+{{\left( 6 \right)}^{2}} \\
& \Rightarrow 48={{\left( BC \right)}^{2}}+36 \\
& \Rightarrow 48-36={{\left( BC \right)}^{2}} \\
& \Rightarrow 12={{\left( BC \right)}^{2}} \\
& \Rightarrow \sqrt{12}=BC \\
\end{align}\]
\[\Rightarrow 2\sqrt{3}=BC\] ………………………………..(8)
In the figure, we can see that the height AB is the summation of the length BC and CA.
So, \[AB=BC+CA\] ………………………………..(9)
From equation (6), equation (8), and equation (9), we get
\[\Rightarrow AB=2\sqrt{3}+4\sqrt{3}=6\sqrt{3}\]
Therefore, the height of the tree is \[6\sqrt{3}\] meters.
Recently Updated Pages
How do you write a polynomial function with the given class 10 physics CBSE

How do you find the integral of left x3 rightleft ln class 10 maths CBSE

Choose the word which is closest to the opposite in class 10 english CBSE

Fill in the blank in the given sentence to complete class 10 english CBSE

Let we have the sum of a series as Sleft K right1+3+5+left class 10 maths CBSE

How do you write the interval 34 as an inequality involving class 10 maths CBSE

Trending doubts
Write an application to the principal requesting five class 10 english CBSE

Why is there a time difference of about 5 hours between class 10 social science CBSE

Write a letter to the principal requesting him to grant class 10 english CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

What is the median of the first 10 natural numbers class 10 maths CBSE

Write examples of herbivores carnivores and omnivo class 10 biology CBSE




