
A starts from a place P to go to a place Q. at the same time B starts from Q to P. if after meeting each other, A and B took 4 hours and 9 hours more respectively to reach their destination, what is the ratio of their speeds?
(a) 3:2
(b) 5:2
(c) 9:4
(d) 9:13
Answer
517.5k+ views
Hint: To solve this question, we will consider a point C’ between places P and Q where A and B meet. We will consider the distance PC as x and CQ as y. After this, we will apply the condition that at the same time A and B course different distances. Also, we will apply the condition of the remaining distances for A and Band how much time they need to cover it.
Complete step-by-step answer:
To solve this question, we will consider here a point C between the points P and Q such that the total distance between P and Q is d as shown:
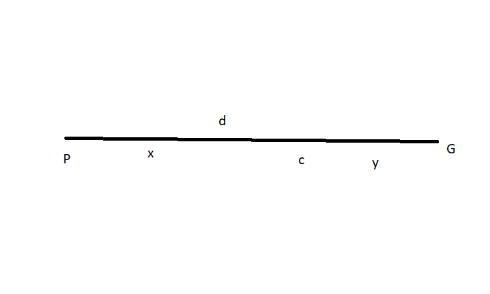
Thus, from above figure we can see that the total distance, d=x+y. therefore:
$\Rightarrow y=d-x...........(i)$
We are given that, now A and B have met at point C. it is further given that the time taken for A to go from point c to point Q is 4 hours. Let us say that the speed of A is ${{V}_{A}}$ then the relation between the distance travelled, velocity and time elapsed is given as
\[\begin{align}
& speed=\dfrac{Total\,distance}{total\,time} \\
& {{V}_{A}}=y \\
& \Rightarrow y=4{{V}_{A}}............(ii) \\
\end{align}\]
Now, we are given that the time taken for B to go to point Q from point A is 9 hours. Thus, the relation between speed, distance travelled and total time taken is given by
$\begin{align}
& {{V}_{B}}=\dfrac{x}{9} \\
& \Rightarrow x=9{{V}_{B}}............(iii) \\
\end{align}$
Where ${{V}_{B}}$= velocity of B
Now, we are given that, initially A takes time t and reach the point C from point P. the same time is also taken by B to reach the point C from point Q. thus, we get the following relation:
$\begin{align}
& x={{V}_{A}}t.............(iv) \\
& y={{V}_{B}}t..............(v) \\
\end{align}$
Now we will divide the equation (iv) by equation (v). After dividing, we will get:
$\begin{align}
& \dfrac{x}{y}=\dfrac{{{V}_{A}}t}{{{V}_{B}}t} \\
& \Rightarrow \dfrac{x}{y}=\dfrac{{{V}_{A}}}{{{V}_{B}}}...........(vi) \\
\end{align}$
Now, we will put the values of x and y from equation (iv) and (v) into the equation (vi). After doing this, we will get following:
\[\dfrac{9{{V}_{B}}}{4{{V}_{A}}}=\dfrac{{{V}_{A}}}{{{V}_{B}}}\]
$\begin{align}
& \Rightarrow 9{{V}_{B}}^{2}=4{{V}_{A}}^{2} \\
& \Rightarrow 3{{V}_{B}}=2{{V}_{A}} \\
& \Rightarrow \dfrac{{{V}_{A}}}{{{V}_{B}}}=\dfrac{3}{2} \\
\end{align}$
So, the correct answer is “Option A”.
Note: Another way of doing this question is as follows when A and B meet at point C, then we can have following relation:
\[{{V}_{A}}t+{{V}_{B}}t=d\]
After meeting, the distance left for $A={{V}_{B}}t$ and the distance left for $B={{V}_{A}}t$. Now according to the question, ${{V}_{B}}t={{V}_{A}}$. Also ${{V}_{A}}t=9{{V}_{B}}$. Therefore we get:
$\dfrac{{{V}_{B}}t}{{{V}_{A}}t}=\dfrac{4{{V}_{A}}}{9{{V}_{B}}}\Rightarrow \dfrac{{{V}_{A}}}{{{V}_{B}}}=\dfrac{3}{2}$
Complete step-by-step answer:
To solve this question, we will consider here a point C between the points P and Q such that the total distance between P and Q is d as shown:

Thus, from above figure we can see that the total distance, d=x+y. therefore:
$\Rightarrow y=d-x...........(i)$
We are given that, now A and B have met at point C. it is further given that the time taken for A to go from point c to point Q is 4 hours. Let us say that the speed of A is ${{V}_{A}}$ then the relation between the distance travelled, velocity and time elapsed is given as
\[\begin{align}
& speed=\dfrac{Total\,distance}{total\,time} \\
& {{V}_{A}}=y \\
& \Rightarrow y=4{{V}_{A}}............(ii) \\
\end{align}\]
Now, we are given that the time taken for B to go to point Q from point A is 9 hours. Thus, the relation between speed, distance travelled and total time taken is given by
$\begin{align}
& {{V}_{B}}=\dfrac{x}{9} \\
& \Rightarrow x=9{{V}_{B}}............(iii) \\
\end{align}$
Where ${{V}_{B}}$= velocity of B
Now, we are given that, initially A takes time t and reach the point C from point P. the same time is also taken by B to reach the point C from point Q. thus, we get the following relation:
$\begin{align}
& x={{V}_{A}}t.............(iv) \\
& y={{V}_{B}}t..............(v) \\
\end{align}$
Now we will divide the equation (iv) by equation (v). After dividing, we will get:
$\begin{align}
& \dfrac{x}{y}=\dfrac{{{V}_{A}}t}{{{V}_{B}}t} \\
& \Rightarrow \dfrac{x}{y}=\dfrac{{{V}_{A}}}{{{V}_{B}}}...........(vi) \\
\end{align}$
Now, we will put the values of x and y from equation (iv) and (v) into the equation (vi). After doing this, we will get following:
\[\dfrac{9{{V}_{B}}}{4{{V}_{A}}}=\dfrac{{{V}_{A}}}{{{V}_{B}}}\]
$\begin{align}
& \Rightarrow 9{{V}_{B}}^{2}=4{{V}_{A}}^{2} \\
& \Rightarrow 3{{V}_{B}}=2{{V}_{A}} \\
& \Rightarrow \dfrac{{{V}_{A}}}{{{V}_{B}}}=\dfrac{3}{2} \\
\end{align}$
So, the correct answer is “Option A”.
Note: Another way of doing this question is as follows when A and B meet at point C, then we can have following relation:
\[{{V}_{A}}t+{{V}_{B}}t=d\]
After meeting, the distance left for $A={{V}_{B}}t$ and the distance left for $B={{V}_{A}}t$. Now according to the question, ${{V}_{B}}t={{V}_{A}}$. Also ${{V}_{A}}t=9{{V}_{B}}$. Therefore we get:
$\dfrac{{{V}_{B}}t}{{{V}_{A}}t}=\dfrac{4{{V}_{A}}}{9{{V}_{B}}}\Rightarrow \dfrac{{{V}_{A}}}{{{V}_{B}}}=\dfrac{3}{2}$
Recently Updated Pages
Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Social Science: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Master Class 11 Physics: Engaging Questions & Answers for Success

Trending doubts
What is a collective noun for bees class 10 english CBSE

Every rational number is a A natural number b An integer class 10 maths CBSE

Why are material sources written sources and oral sources class 10 social science CBSE

Fill in the blanks Least polluting fuel for vehicles class 10 chemistry CBSE

How does Tommy describe the old kind of school class 10 english CBSE

Choose the most suitable one word for the following class 10 english CBSE




