
A semi-infinite insulating rod has linear charge density $ \lambda $ . The electric field at the point P shown in figure is :-

(A) $ \dfrac{{2{\lambda ^2}}}{{{{\left( {4\pi {\varepsilon _0}r} \right)}^2}}} $ at $ {45^ \circ } $ with AB
(B) $ \dfrac{{\sqrt 2 \lambda }}{{\left( {4\pi {\varepsilon _0}{r^2}} \right)}} $ at $ {45^ \circ } $ with AB
(C) $ \dfrac{{\sqrt 2 \lambda }}{{\left( {4\pi {\varepsilon _0}r} \right)}} $ at $ {45^ \circ } $ with AB
(D) $ \dfrac{{\sqrt 2 \lambda }}{{\left( {4\pi {\varepsilon _0}r} \right)}} $ at perpendicular with AB

Answer
490.8k+ views
Hint: We will calculate the x-component and the y-component of the electric field at the point P, as shown in the figure, due to the semi-infinite insulating rod carrying uniform linear charge of density $ \lambda $ .We integrate the electric field $ d{E_x} $ over the length of the “semi-infinite” rod that is with respect to the variable $ x $ from 0 to $ \infty $ .
Complete step by step answer:
It has been given that a semi-infinite insulating rod has linear charge density $ \lambda $ .
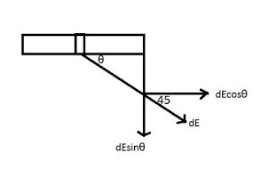
Consider an infinitesimal charge element of length $ dx $ at distance $ x $ from the end of the rod as shown in the figure.
$ \cos \theta = \dfrac{x}{{\sqrt {{r^2} + {x^2}} }} $ by Pythagoras Theorem, which states that the square of the hypotenuse is equal to the square of the other two sides of a right angled-triangle.
As the direction of electric field due to a charge element is along the line joining the element to the point where the field is to be calculated.
From the figure, the x-component of the field will be,
$ d{E_x} = dE\cos \theta $
$ \Rightarrow d{E_x} = \dfrac{{\lambda dx}}{{\left( {{r^2} + {x^2}} \right)}} \times \dfrac{x}{{\sqrt {{r^2} + {x^2}} }} $
Integrating $ d{E_x} $ over the length of the “semi-infinite” rod that is with respect to the variable $ x $ from 0 to $ \infty $ , we get
$ \int {d{E_x}} = k\lambda \int {\dfrac{{xdx}}{{{{\left( {{r^2} + {x^2}} \right)}^{{\raise0.7ex\hbox{ $ 3 $ } \!\mathord{\left/
{\vphantom {3 2}}\right.}
\!\lower0.7ex\hbox{ $ 2 $ }}}}}}} $
For simplicity we take $ t = {r^2} + {x^2} $ .
Thus, $ dxdx = dt $ .
On simplifying the equation, we can get,
$ \int {d{E_x}} = k\lambda \int {\dfrac{{dt}}{{{{\left( t \right)}^{{\raise0.7ex\hbox{ $ 3 $ } \!\mathord{\left/
{\vphantom {3 2}}\right.}
\!\lower0.7ex\hbox{ $ 2 $ }}}}}}} $ .
By rules of integration,
$ \int {dE} = \dfrac{{k\lambda }}{2} \times \dfrac{{ - 3}}{2}{t^{ - {\raise0.7ex\hbox{ $ 1 $ } \!\mathord{\left/
{\vphantom {1 2}}\right.}
\!\lower0.7ex\hbox{ $ 2 $ }}}} $ .
Substituting, the value of $ t = {r^2} + {x^2} $ , and setting limits of integration at 0 and $ \infty $ ,
$ \int {d{E_x}} = k\lambda \left[ {\dfrac{1}{{\sqrt {{r^2} + {x^2}} }}} \right]_0^\infty $
$ \Rightarrow {E_x} = \dfrac{{k\lambda }}{r} $
We note that $ \left| {{E_x}} \right| = \left| {{E_y}} \right| $ for all $ r $ .
Therefore, the angle that the electric field vector makes at P is
$ \tan \theta = \dfrac{{\left| {{E_x}} \right|}}{{\left| {{E_y}} \right|}} $ .
Since $ \left| {{E_x}} \right| = \left| {{E_y}} \right| $ , $ \tan \theta = 1 $ .
It implies that $ \theta = {45^ \circ } $ and is independent of $ r $ , that is the distance of the point P from the edge of the “semi-infinite” rod.
Now, the net electric field is given by, $ {E_{net}} = \sqrt {{E_X}^2 + {E_Y}^2} = \sqrt 2 \dfrac{{k\lambda }}{r} $ where $ k = \dfrac{1}{{4\pi {\varepsilon _0}}} $ is a constant.
Hence the net electric field is $ \dfrac{{\sqrt 2 \lambda }}{{\left( {4\pi {\varepsilon _0}r} \right)}} $ at $ {45^ \circ } $ with AB.
The correct answer is Option C.
Note:
Electric field is defined as the electric force per unit charge. The direction of the field is taken to be the direction of the force it would exert on a positive test charge. The electric field is radially outward from a positive charge and radially in toward a negative point charge.
Complete step by step answer:
It has been given that a semi-infinite insulating rod has linear charge density $ \lambda $ .

Consider an infinitesimal charge element of length $ dx $ at distance $ x $ from the end of the rod as shown in the figure.
$ \cos \theta = \dfrac{x}{{\sqrt {{r^2} + {x^2}} }} $ by Pythagoras Theorem, which states that the square of the hypotenuse is equal to the square of the other two sides of a right angled-triangle.
As the direction of electric field due to a charge element is along the line joining the element to the point where the field is to be calculated.
From the figure, the x-component of the field will be,
$ d{E_x} = dE\cos \theta $
$ \Rightarrow d{E_x} = \dfrac{{\lambda dx}}{{\left( {{r^2} + {x^2}} \right)}} \times \dfrac{x}{{\sqrt {{r^2} + {x^2}} }} $
Integrating $ d{E_x} $ over the length of the “semi-infinite” rod that is with respect to the variable $ x $ from 0 to $ \infty $ , we get
$ \int {d{E_x}} = k\lambda \int {\dfrac{{xdx}}{{{{\left( {{r^2} + {x^2}} \right)}^{{\raise0.7ex\hbox{ $ 3 $ } \!\mathord{\left/
{\vphantom {3 2}}\right.}
\!\lower0.7ex\hbox{ $ 2 $ }}}}}}} $
For simplicity we take $ t = {r^2} + {x^2} $ .
Thus, $ dxdx = dt $ .
On simplifying the equation, we can get,
$ \int {d{E_x}} = k\lambda \int {\dfrac{{dt}}{{{{\left( t \right)}^{{\raise0.7ex\hbox{ $ 3 $ } \!\mathord{\left/
{\vphantom {3 2}}\right.}
\!\lower0.7ex\hbox{ $ 2 $ }}}}}}} $ .
By rules of integration,
$ \int {dE} = \dfrac{{k\lambda }}{2} \times \dfrac{{ - 3}}{2}{t^{ - {\raise0.7ex\hbox{ $ 1 $ } \!\mathord{\left/
{\vphantom {1 2}}\right.}
\!\lower0.7ex\hbox{ $ 2 $ }}}} $ .
Substituting, the value of $ t = {r^2} + {x^2} $ , and setting limits of integration at 0 and $ \infty $ ,
$ \int {d{E_x}} = k\lambda \left[ {\dfrac{1}{{\sqrt {{r^2} + {x^2}} }}} \right]_0^\infty $
$ \Rightarrow {E_x} = \dfrac{{k\lambda }}{r} $
We note that $ \left| {{E_x}} \right| = \left| {{E_y}} \right| $ for all $ r $ .
Therefore, the angle that the electric field vector makes at P is
$ \tan \theta = \dfrac{{\left| {{E_x}} \right|}}{{\left| {{E_y}} \right|}} $ .
Since $ \left| {{E_x}} \right| = \left| {{E_y}} \right| $ , $ \tan \theta = 1 $ .
It implies that $ \theta = {45^ \circ } $ and is independent of $ r $ , that is the distance of the point P from the edge of the “semi-infinite” rod.
Now, the net electric field is given by, $ {E_{net}} = \sqrt {{E_X}^2 + {E_Y}^2} = \sqrt 2 \dfrac{{k\lambda }}{r} $ where $ k = \dfrac{1}{{4\pi {\varepsilon _0}}} $ is a constant.
Hence the net electric field is $ \dfrac{{\sqrt 2 \lambda }}{{\left( {4\pi {\varepsilon _0}r} \right)}} $ at $ {45^ \circ } $ with AB.
The correct answer is Option C.
Note:
Electric field is defined as the electric force per unit charge. The direction of the field is taken to be the direction of the force it would exert on a positive test charge. The electric field is radially outward from a positive charge and radially in toward a negative point charge.
Recently Updated Pages
How is Abiogenesis Theory Disproved Experimentally?

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 10 Computer Science: Engaging Questions & Answers for Success

Master Class 10 General Knowledge: Engaging Questions & Answers for Success

Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Master Class 9 English: Engaging Questions & Answers for Success

Trending doubts
Which are the Top 10 Largest Countries of the World?

Why is the cell called the structural and functional class 12 biology CBSE

a Tabulate the differences in the characteristics of class 12 chemistry CBSE

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE

What are the major means of transport Explain each class 12 social science CBSE

What is the Full Form of PVC, PET, HDPE, LDPE, PP and PS ?




