
A right triangle has a hypotenuse of length \[p\] cm and one side of length \[q\] cm. If \[p - q = 1\] , find the length of the third side of the triangle if \[p = 5\] and \[q = 4\]
Answer
564.9k+ views
Hint: To solve this question, to calculate the third side of a right-angled triangle we use the Pythagoras theorem.
Complete step-by-step answer:
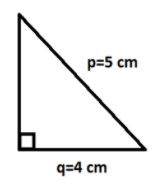
In the question, it is given that the hypotenuse is of length \[p\] cm and one side is of length \[q\] cm.
So, Hypotenuse \[ = p\] cm and Base \[ = q\] cm as shown in the figure.
So, now we will use Pythagoras theorem.
Pythagoras theorem states that “In a right-angled triangle, the square of the hypotenuse side is equal to the sum of squares of the other two sides.“ The sides of this triangle have been named as Perpendicular, Base and Hypotenuse.
So, \[Hypotenus{e^2} = Bas{e^2} + Perpendicula{r^2}\]
\[{p^2} = {q^2} + Perpendicula{r^2}\]
\[Perpendicula{r^2} = {p^2} - {q^2}\]
Now, we will put \[p = 5\] and \[q = 4\] in the above formed equation, we get
\[Perpendicula{r^2} = {5^2} - {4^2}\]
Or, \[Perpendicula{r^2} = 25 - 16\]
Or, \[Perpendicula{r^2} = 9\]
Therefore, \[Perpendicular = 3\]
Thus, the length of the third side of the triangle is equal to \[3\] cm.
Note: Keep in mind the Pythagoras theorem. The Pythagorean equation relates the sides of a right triangle in a simple way, so that if the lengths of any two sides are known the length of the third side can be found. Another corollary of the theorem is that in any right triangle, the hypotenuse is greater than any one of the other sides, but less than their sum.
Complete step-by-step answer:

In the question, it is given that the hypotenuse is of length \[p\] cm and one side is of length \[q\] cm.
So, Hypotenuse \[ = p\] cm and Base \[ = q\] cm as shown in the figure.
So, now we will use Pythagoras theorem.
Pythagoras theorem states that “In a right-angled triangle, the square of the hypotenuse side is equal to the sum of squares of the other two sides.“ The sides of this triangle have been named as Perpendicular, Base and Hypotenuse.
So, \[Hypotenus{e^2} = Bas{e^2} + Perpendicula{r^2}\]
\[{p^2} = {q^2} + Perpendicula{r^2}\]
\[Perpendicula{r^2} = {p^2} - {q^2}\]
Now, we will put \[p = 5\] and \[q = 4\] in the above formed equation, we get
\[Perpendicula{r^2} = {5^2} - {4^2}\]
Or, \[Perpendicula{r^2} = 25 - 16\]
Or, \[Perpendicula{r^2} = 9\]
Therefore, \[Perpendicular = 3\]
Thus, the length of the third side of the triangle is equal to \[3\] cm.
Note: Keep in mind the Pythagoras theorem. The Pythagorean equation relates the sides of a right triangle in a simple way, so that if the lengths of any two sides are known the length of the third side can be found. Another corollary of the theorem is that in any right triangle, the hypotenuse is greater than any one of the other sides, but less than their sum.
Recently Updated Pages
Identify the correct word from the given options which class 10 english CBSE

Find the synonym of the underlined word Excessive exposure class 10 english CBSE

Fill in the blank with suitable prepositions He apologised class 10 english CBSE

How did the economic trends of the 1920s help cause class 10 social science CBSE

Which of the following compounds is formed when Na2SO3 class 10 chemistry CBSE

You are SimarSmriti of Lotus International School Jodhpur class 10 english CBSE

Trending doubts
Why is there a time difference of about 5 hours between class 10 social science CBSE

Tropical deciduous trees shed their leaves in the dry class 10 social science CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

Write a letter to the principal requesting him to grant class 10 english CBSE

The uses of bleaching powder are A It is used bleaching class 10 chemistry CBSE

Leap year has days A 365 B 366 C 367 D 368 class 10 maths CBSE




